0591

593

§ 2. Zbieżność jednostajna całek

7) Wykazać, że całki

i    i

(a) J x^,-'dx,    (b) J x'~^,ln"xdx

o    o

(w jest liczbą naturalną) są dla x = 0 zbieżne jednostajnie wzglądem p w obszarze p>p_o>0 i niejednostajnie w obszarze p>0.

Majorantami w obszarzep>p_o>0 są: (a)    (b) x^,0~' |ln jtI". Z drugiej strony, dla każdej liczby

rjconst

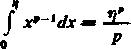
oo, gdy p-* 0.

8) Analogicznie można wykazać, że całka

/ x’-^l(l-x)'~ⁱdx o

jest przy x = 0 zbieżna jednostąjnie wzglądemp dla p>po>0 i (przy x — 1) względem q dla q>q₀>0.

9) Udowodnić, że zbieżność całki

f 22-?-dx

J x»

przyjc= Ojest jednostajna względem y dla y<y₀<2 i nie jest jednostajna dla y<2.

Dla przypadku y<y₀<2 majorantą jest —^—. Weźmy teraz liczbą q>0 tak małą, żeby dla x<q

x^,«~¹

spełniona była nierówność > -y. Wówczas

•»

/•

• dx >

i/-

dx

1

2 J X”-’    2(2-y)

o

gdy

■2.

10) Dowieść, że całka

J(l+jH-x^ł-|- ... -M"-')

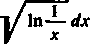
dla x = 0 i dla x — 1 jest zbieżna jednostajnie względem n (n = 1,2, 3, ...).

Ponieważ 1—f-jc-f-je²-!- ...    ^ , majorantą jest funkcja -j-jy

dziale <0, 1> jest całkowalna.

11) Wykazać bezpośrednio, że zbieżność całki

Y

In-j

która w prze-

dx

T y²-x² J (x²+y²)²

(dla x — 0) nie jest jednostajna wzglądem y w przedziale <0,1>. Dla dowolnego q — const jest

(x²+y²)-

■dx ■■

x²+y²

X-tl

»0

_a_

tj²+y²

gdy y—► 0.