0601

§ 3. Wykorzystanie zbieżności jednostajnej całek

603

jest zatem ostatecznie

h

A

4k

8) Obliczyć całki (Legendre’a)

00

w/

O

sin mx e^2nx-l

dx,

(b) f    dx {m> 0).

„

Rozwiązanie, (a) Rozwinięcie

sin mx e^inx—l

£ e~^2rK1 sin mx

V-1

jest także zbieżne jednostajnie w dowolnym przedziale </), <4>; sumy częściowe szeregu mąją jako majo-rantę funkcję ^^sin mx^ . Możemy wobec tego całkować szereg wyraz za wyrazem

00

/

00

S

v-l

_m_

m^ł+4i»²7c²

_|    J

V-l 0

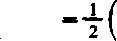
1

eT-1

■ +

ł)

1 e"+l 1 ₍,x 4 «■—1    2 m

(b) Analogicznie otrzymujemy

/

sin mx

e^2łl1-f-l

dx

oo

m²+4y²7t²

1

2m

gm/I

ź==»«-

Uwaga. Naturalną drogą rozwiązania tego zadania byłoby także rozwinięcie w szereg funkcji sin mx. W przypadku (a) na przykład, doszlibyśmy wówczas do całek rozpatrzonych w zadaniu 7 i dla uzyskania wyników w postaci skończonej można by było skorzystać ze znanego rozwinięcia

oo

1

e"-l

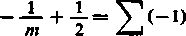
B_k

2 k\

k-1

m^2k~¹

[449]. Ta droga jednak ma zasadniczą wadę — należałoby założyć, że m<2n, podczas gdy wynik jest prawdziwy dla dowolnego m.

9) Jeżeli w elementarnej równości [492, 2°]

(2/»—3)!! ji (2n-2)!! ' 2

dx

(1 +x²)"

T

podstawimy x = ~ , to otrzymamy

Vń

i’ ^dz = (2/1-3)!!

) / (2«—2)!! ^V 2'

1

Te wyniki zadań (a) i (b) otrzymuje się korzystając z rozwinięcia na ułamki proste funkcji ctgh x 1/sinh a: [441, 10].