0607

609

§ 3. Wykorzystanie zbieżności jednostajnej całek

(b) Inna interesująca funkcja — funkcja Bessela pierwszego rodzaju J₀(x), ma rozwinięcie [441, 4), 5)1

/oW = i+V(-i

4—I    fvn».2^ł»

_v_,    (v!)² •2^2ł

które może być też utworzone w ten sam sposób jak rozwinięcie funkcji g (x). Weźmy mianowicie

a₀ = 1, a_łv = (—l)*¹ (2v~^1)!! ,    a,,-! = 0.

(2v)!l

Wzór (9) daje teraz

cc

o

OD

(2r—1)!! (2t>)!!

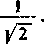
Skorzystaliśmy tu z rozwinięcia funkcji I/|/l +x w szereg dwumienny, w którym przyjęliśmy x = 1.

Uwaga. Pouczające będzie zanalizowanie, czym się w istocie różnią rozumowania z ostatnich dwu przykładów od rozumowań z innych przykładów, w których też całkowaliśmy szeregi wyraz za wyrazem w przedziale nieskończonym.

Wróćmy do ogólnego zagadnienia przejścia do granicy pod znakiem całki w przedziale nieskończonym [518]. Okazuje się ono równoważne istnieniu i równości obu granic iterowanych dla funkcji F(A, y) dwu argumentów [patrz wzór (13)]. Zgodnie z ogólnym twierdzeniem z ustępu 505, warunkiem wystarczającym dla takiej równości granic iterowanych przy założeniu, że istnieją granice pojedyncze, jest zbieżność jednostajna funkcji do jednej z tych granic — do granicy (4) (jednostajna względem A) lub do granicy (5) (jednostajna względem y), obojętnie przy tym do której.

Zazwyczaj zakładaliśmy, że jednostajna jest zbieżność do granicy (5), co odpowiadało zbieżności jednostajnej całki, której górną granicą całkowania była oo. Jednak teza twierdzenia 1 pozostaje w pełni prawdziwa, gdy zamiast tego założymy, że funkcja F dąży jednostajnie do granicy (4)!

00

W przypadku szeregu £ u„(x), którego sumami częściowymi są /„(x), mamy zatem dwie możliwości,

i

Możemy mianowicie wykazać, że przy A -*■ oo funkcja

F.(A) = / /„(*) dx

dąży do granicy ff,(x) dx jednostajnie względem n, czyli że całki te są zbieżne jednostajnie — tak właśnie

a

postępowaliśmy zazwyczaj. Zamiast tego możemy też wykazać, że przy n -> oo funkcja F„(A) dąży do gra-

A

nicy J <p (x) dx jednostajnie względem A, czyli że jest zbieżny jednostajnie względem A szereg

a

/ ««(•*) dx = f cp (X) dx .

n— 1 ■    a

Ta droga okazała się wygodniejsza w przykładach 13 i 14!

520. Ciągłość i różniczkowalność całki względem parametru. Tutaj też zajmiemy się najpierw przeniesieniem twierdzeń 2 i 3 z ustępów 506 i 507 na przypadek przedziału nieskończonego.

39 Rachunek różniczkowy