0605

607

§ 3. Wykorzystanie zbieżności jednostajnej całek

Gdyby tu wolno było całkować wyraz za wyrazem, to od razu otrzymalibyśmy wynik

I=Y~

Z_i ni J    X    2Zj b! 2

*-10    N-1

Ale uzasadnienie, że można tak całkować, wymaga w tym przypadku nietypowego rozumowania. Ponieważ szereg stojący pod znakiem całki ma jako majorantę szereg

V-0

o wyrazach stałych, to w skończonym przedziale <0, A} wolno całkować wyraz za wyrazem:

co    *4

f y £.. muŁ dx - yi r żm dx=y r -słl* .

J n! x    Z_i n\ ■> x    i—i n\ J t

A <0    co    A

(8)

°° in /

Pozostaje przejść do granicy przy A -*■ oo. Łatwo jest dostrzec, że z istnienia całki /-dt wynika,

o *

*0 . ^

że całka J —y dt jest dla wszystkich wartości /_o>0 jednostajnie ograniczona.

ir

sin t

dt\ < Ł.

Szereg (8), którego wyrazy zależą od A, jest wobec tego majoryzowany przez szereg o wyrazach stałych

. VML Zj n! ’

lal'

a więc jest zbieżny jednostajnie względem A. Na podstawie znanego twierdzenia [433] można zatem w tym szeregu, przy A-*- oo, przejść do granicy wyraz za wyrazem. Dowód jest tym samym zakończony.

14) Inny przykład tego samego rodzaju. Dany jest szereg zbieżny

Tworzymy dla *>0 nowy szereg

CO

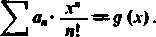
*-0

Szereg ten jest także zbieżny i przy tym jest zbieżny jednostajnie w dowolnym skończonym przedziale <0, Ay — wynika to z kryteriów Abela i Dirichleta [430], bo czynnik x■/»! maleje wraz ze wzrostem n przynajmniej dla n>A.

Dowieść, że

CO

f e~*g (*) dx*= s, o