0559

561

§ S. Przybliżone obliczanie całek niewłaściwych

Jeżeli otrzymany wzór podzielimy wyraz za wyrazem przez —e^,x i porównamy oddzielnie części rzeczywiste i urojone po obu stronach równości, to otrzymamy dogodniejsze do obliczeń wzory

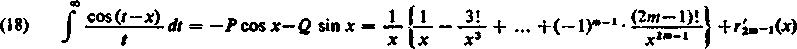
X

oraz

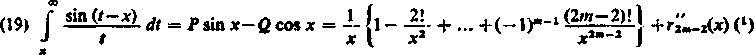
gdzie odpowiednio

rim-tW ~ (—l)"(2m+l)! J

co

¹ _f2m+l

oraz

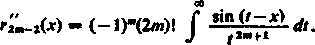
M

Łatwo wykazać (na przykład korzystając ze wzoru Bonneta, 306 (3)), że

x

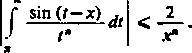
Przechodząc do granicy dla X -*■ oo stwierdzimy, że reszty we wzorach (18) i (19) są co do wartości bezwzględnej odpowiednio nie większe niż podwojony wyraz następny odpowiedniego rozwinięcia. Stąd widać wyraźnie, że po przedłużeniu rozwinięć (18) i (19) do nieskończoności otrzymamy przedstawienia asymptotyczne całek, występujących po lewej stronie tych wzorów.

W szczególności, na przykład z (19) otrzymamy po podstawieniu x = kit (k = 1, 2, 3,...)

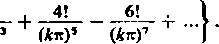
p_t = si (**)=- { J!5±    (_|)*₊«{J-+-2L

J t    | *7e (kit)

Stąd możemy już łatwo otrzymać dla k>7 przybliżone wartości

p₃ = 0,1040, p₄ = -0,0786, p_s = 0,0631, p„ = -0,0528, ..

(') Ciekawe, że wyrazy w nawiasie klamrowym {...} są właśnie odwrotnościami wyrazów znanych rozwinięć sinusa i kosinusa w szeregi potęgowe [404 (12) i (13)].