0533

535

§4. Specjalne metody obliczania całek niewłaściwych

Przykłady

1) W przypadku całki

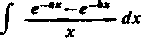
o

mamy

/ W = e-*,    /(0)=1,    /(+«) = 0,

a więc wartość całki wynosi In —■.

a

2) Dana jest całka

/ ^ln

p+qę-‘*

p+qe~^bx

dx

x

(p,q>0).

Zastępując logarytm ilorazu różnicą logarytmów możemy przyjąć tu f{x) — ln (j>+qe~*), a więc /(O) *= = In (p-hq) i /(+ oo) = lnp.

Odpowiedź, ln    ln .

3) Obliczyć całką

I

arc tg ojc—arc tg bx ^ x

Mamy w tym przypadku

f(x) = arc tg x, /(O) = 0,    /(+ oo) = -i- re.

Odpowiedź. ~ ln —.

Z u

II. Czasami funkcja f(x) nie ma granicy skończonej dla x-* +oo, istnieje natomiast całka

+00

Zastępując w podanych rozważaniach od razu A przez + oo, otrzymamy zamiast (4) wynik

<4a)

J    x    a

Przykład 4)

/

cos ax—cos bx    _ j_n b_

(gdyż całka J -dz, jak wiemy, istnieje).

o ²

III. Analogicznie, gdy funkcja f(x) jest nieciągła w punkcie x=0, lecz istnieje całka

A

j £^-dz (A < +oo),