0555

557

§ 5. Przybliżone obliczanie całek niewłaściwych

Najczęściej wygodniej jest przekształcić całkę J tak, by miała skończone granice całkowania lub roz-

a

A CO

łożyć ją na dwie całki J+J i przekształcić w taki sposób tę drugą.

m A

<o

2)    Weźmy znów tę samą całkę / = J e~^x1 dx i przedstawmy ją w postaci sumy

O

CO    1    CO

/ = / + /= h+Il.

o o 1

/1 obliczymy według wzoru Simpsona biorąc 2n = 10 i pięć cyfr po przecinku; |/?|<0,00001, h = 0,746830_to,00002. h przekształcimy za pomocą podstawienia x -- 1// i otrzymamy

O

Obliczymy zwykłymi metodami I₂ x 0,13945, a więc I x 0,88628.

Oszacowaniem błędu nie będziemy się zajmowali.

Gdy całka w przedziale nieskończonym ma punkt osobliwy, również w skończoności należy rozłożyć przedział na dwa, zawierające tylko jedną osobliwość.

3)    Rozpatrzmy (dla 0«j<1) całkę

co    1    co

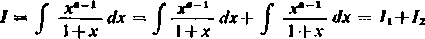
O    Ol

Całkę Ii obliczamy wydzielając osobliwości

1    1

ii = f (x^t-‘-x^a+x‘^+l-x‘+²+y+³)dx- f J£H.dx=‘ iu-i,t.

J    J l

o    o

In = —---TT -1--7-5---77T H--7-7-. a Ii 2 obliczamy według wzoru Simpsona.

a a+1    o-i-2    o+3    o+4

i/2

Niech na przykład o =    — = 0,7071068...; wtedy /_u = 1,14052... Dla /₁₂ (2o = 10, pięć cyfr po

przecinku) otrzymujemy wartość 0,09518. A więc I_t « 1,04534.

Całkę I₂ sprowadzamy za pomocą podstawienia x = 1/r do postaci

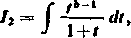
o

gdzie b = 1— a = 0,2928931... Tak samo jak poprzednio otrzymamy I₂ ss 2,90289. Ostatecznie I x

x 3,94823. Później [522, 1°1 dowiemy się, że prawdziwa wartość / wynosi -7-^— = 3,948246...

sin 7ta

OO

Czasem w przypadku wolno zbieżnej całki j f(x) dx może się udać wydzielenie z niej (na przykład

a

całkując kilkakrotnie przez części) łatwych od obliczenia wyrazów, w ten sposób, ażeby pozostała całka była już bardzo mała.