0625

$ 3. Wykorzystanie zbieżności jednostajnej całek

627

istnienie i ciągłość całek dla wszystkich wartości a wynika z istnienia majoranty e^-*¹. Według reguły Leibniza

± = - f c-¹ sin «L - iŁ dx = -2 f    sin    0- = ^-).

da. J    x² x*    J    x

o    o

Druga całka jest dla wszystkich wartości a zbieżna jednostajnie w punktach y = 0 i y = oo i wobec tego pierwsza całka jest zbieżna jednostajnie w punktach x = oo i x = O dla * spełniających nierówność 0<a_o<«</4< + oo. Wobec tego stosowanie reguły Leibniza jest przy <%>0 dozwolone.

Dalsze różniczkowanie względem a (dopuszczalność uzasadnimy analogicznie) prowadzi do równości

d²u

da²

00 00 2 j sin y² dy = 4 J e' o    >

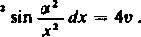
Dokładnie tak samo otrzymujemy

d² v da²

—Au.

Przyjmując w = u-fiu otrzymujemy dla w równanie różniczkowe

d²w

d<x²

—Aiw.

Równanie charakterystyczne 2^I+4f = 0 ma pierwiastki X = ±|/2=F|/2/. Ogólne rozwiązanie równania różniczkowego ma zatem postać

w = u+iv = Ae^-*^² (cos a j/T+i sin a ^2 )+Be²^² (cos a tfl—i sin » )/l) .

Ponieważ funkcja w jest ograniczona dla wszystkich wartości *, to B = 0. Dalej, dla « — 0 powinno być w =    , skąd A — -Ł—-. Ostatecznie

u = J^-e~**^cos ot ^2, v = £Le~*'f^rsin * l/T.

2 2

11) Udowodnić tożsamość

a C e ^1,1 dx ^xl+a2

(o > 0).

Oznaczymy całkę z lewej strony przez u, a całkę z prawej przez u. Podstawiając x² +a² = y² w całce n doprowadzamy ją do postaci

oo

« = «*’■ J e~*²dy.

a

W całce v wprowadzamy nową zmienną podstawiąjąc x = az; otrzymujemy

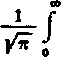
e-^vdz

z²+1 '

v —