0619

621

S 3. Wykorzystanie zbieżności jednostajnej odek

2) Za pomocą różniczkowania względem parametru obliczyć całki (a, /?, k>0)

(a) J = F — ^coaoi-e-^k*dx, (b) H= f    ■ ““i* e-"dx.

J x    J x    x

o    o

Rozwiązanie, (a) Pochodna J względem a wyraża się całką

Ot

a² + k² ’

= f e~^ix sin <xx dx dx J

która jest zbieżna jednostajnie względem ot. Stąd

J = ^\n(a²+k²)+C.

Ponieważ dla ot = 0 całka J jest równa zeru, więc C = £ ln k² i ostatecznie

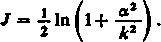
(b) Różniczkując H względem <x pod znakiem całki otrzymujemy

dH

doi

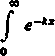
sin fix cos *x x

dx.

Stosowanie reguły Leibniza jest tu dozwolone, bo spełnione są, jak łatwo sprawdzić, założenia twier dzenia 3.

Przekształcając iloczyn sin fix cos ot* na różnicę dwu sinusów sprowadzamy otrzymaną całkę do znanych nam już całek [522, 2°]:

ŚŁ-±.\ -sin (<*+/?)* _dx_ F _g->x . gin («-J) x _dx\^J_(_{arc tg} «±£ __{arc tg} «=£) ,

da 2 [J    x    J    x    J 2 \    k    k /

0    o

Całkujemy teraz względem a

h, *±i_mtg 2±l -    i,„^±g^ai_+c.

Stała C = 0, bo dla a = 0 jest H= 0.

3) Obliczyć całkę

J ——-— cos / dl. o

Wskazówka. Wprowadzić parametr i rozpatrzyć ogólniejszą całkę

«0

/I _p~^at

--cos t dt ;

i

obliczyć tę całkę za pomocą różniczkowania i następnie przyjąć a — 1. Odpowiedź. In }/l.