0363

365

§ 1. Zbieżność jednostajna

Inaczej wygląda sprawa z funkcjami rozpatrzonymi w 1); nie podajemy ich wykresów, bo na przykład dla n — 4 lub n = 40 można je otrzymać z wykresów podanych na rysunku 59 zmniejszając wszystkie rzędne odpowiednio 4 lub 40 razy. W tym przypadku krzywe od razu w całej rozciągłości przywierają do osi x.

Podamy teraz podstawową definicję.

Jeżeli 1° ciąg (1) ma w DC funkcję graniczną/(jr) i 2° dla każdego £ > 0 istnieje taki niezależny od x wskaźnik N, że dla n > N nierówność (5) jest spełniona dla wszystkich .Y z 9l jednocześnie, to mówimy, że ciąg (I) jest zbieżny [lub że dąży] do funkcji f (*) jednostajnie względem x w obszarze 9C.

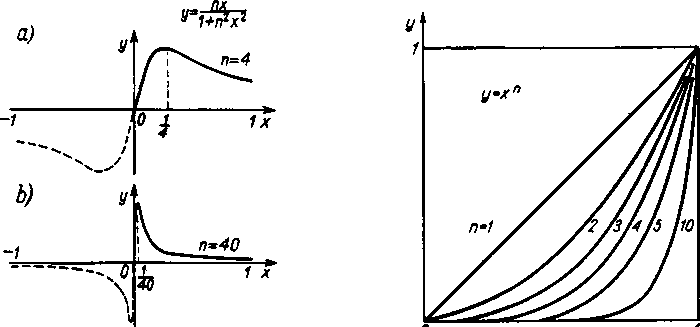
0

Hys. 59

Rys. 60

1 x

Tak więc w pierwszym z podanych przykładów f„(x) dąży do zera jednostajnie względem x w przedziale <0, 1>, a w drugim nie.

Trzeba powiedzieć, że i dla innych funkcji rozpatrywanych w poprzednim ustępie zbieżność nie jest jednostajna. Wykażemy to.

3) Dla funkcji /„(*) = .v" [427, 1)] nierówność a^-" < e(dla e < l)nie może być spełniona jednocześnie dla wszystkich x < 1, co widać chociażby z tego. że x“—> 1, gdy (przy ustalonym n) x -* 1. Na rysunku 60 uwidoczniony jest ten swoisty charakter naruszenia jednostąjności; funkcja graniczna zmienia się tam skokiem, a garb jest nieruchomy.

Niech

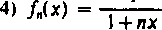
lub

5) f„(x) = 2n²x • e-"**¹.

Niemożliwość w przedziale <0, 1> jednostajnego przybliżenia do funkcji granicznej, która w obu przypadkach dla x > 0 jest równa 0. wynika z tego, że odpowiednio

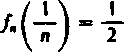
lub