25853

A V A e>0S>0 icc(a.b)

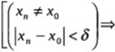
(|\f(x)-g\<€) .

Rys. 2.1.2

Ilustracja definicji Cauchy’ego granicy właściwej funkcji w punkcie

Obrazowo, funkcja f ma w punkcie Xo granicę właściwą g, gdy jej wartości różnią się dowolnie mało od granicy, o ile jej tylko argumenty leżą dostatecznie blisko punktu xo(rys. 2.1.2).

Def. 2.1.4 (Heinego granicy lewostronnej właściwej funkcji w punkcie)

Niech funkcja f będzie określona na przedziale (a,b), -«> < a < b < °o, z wyjątkiem być może punktu xo e (o,bj. Liczba g jest granicą właściwą lewostronną funkcji f w punkcie xo, co zapisujemy

lim f(x) = g

*-*Xj    '

wtedy i tylko wtedy, gdy

(lim f(x_n) = g|

x_n < x₀ dla każdego ne N lim x = x_n

Rys. 2.1.3

Ilustracja definicji Heinego granicy lewostronnej właściwej funkcji w punkcie

Obrazowo, liczba g jest granicą lewostronną funkcji f w punkcie Xo, gdy jej wartości odpowiadające aigumentom dążącym do punktu xo przez wartości mniejsze od xo, dążą do liczby g (rys. 2.1.3). Zamiast równości f(^x) ⁼ 9 stosowany jest także zapis f{x₀ - 0) = g lub f (xć) = g .

Uwaga. Podobnie jak w poprzednich definicjach, wartość funkcji w punkcie Xo (o ile istnieje) nie ma wpływu na granicę lewostronną funkcji w punkcie xo. Granicę prawostronną funkcji f w punkcie

xo definiuje się analogicznie. Oznaczamy ją symbolem j^2^(^x) ⁼ 0,    f(.x_Q+0) = g lub

f(*Z) = 9-

Def. 2.1.S (Cauchy’ego granicy lewostronnej właściwej funkcji w punkcie)

Niech funkcja f będzie określona na przedziale (a, b), -°o < a < b <°o, z wyjątkiem być może punktu