31239

Edited by Foxit PDF Editor

Copyright (c) by Foxit Software Company, 2003 - 2009 For Evaluatk>n Onły.

Ko/.kład jednostajny na odcinku '0.1] — pr/yklad obliczeń

Czas oczekiwania na autobus- zmienna losowa Y ~ (/(0,1). Prawdopodobieństwo P(g < Y < 5) jest równe:

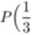
<Y <

i) . r

y»/3

1 dx =

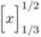
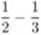
1

6

Prawdopodobieństwa od pow kulające nierównościom ostrym i słabym

Dla zmiennej losowej X o rozkładzie typu ciągłego mamy:

P(a < X < 6) = P(a < X < b) = P(a < X < b) = P{a < X < b).

Równość ta wynika z własności całki oznaczonej.

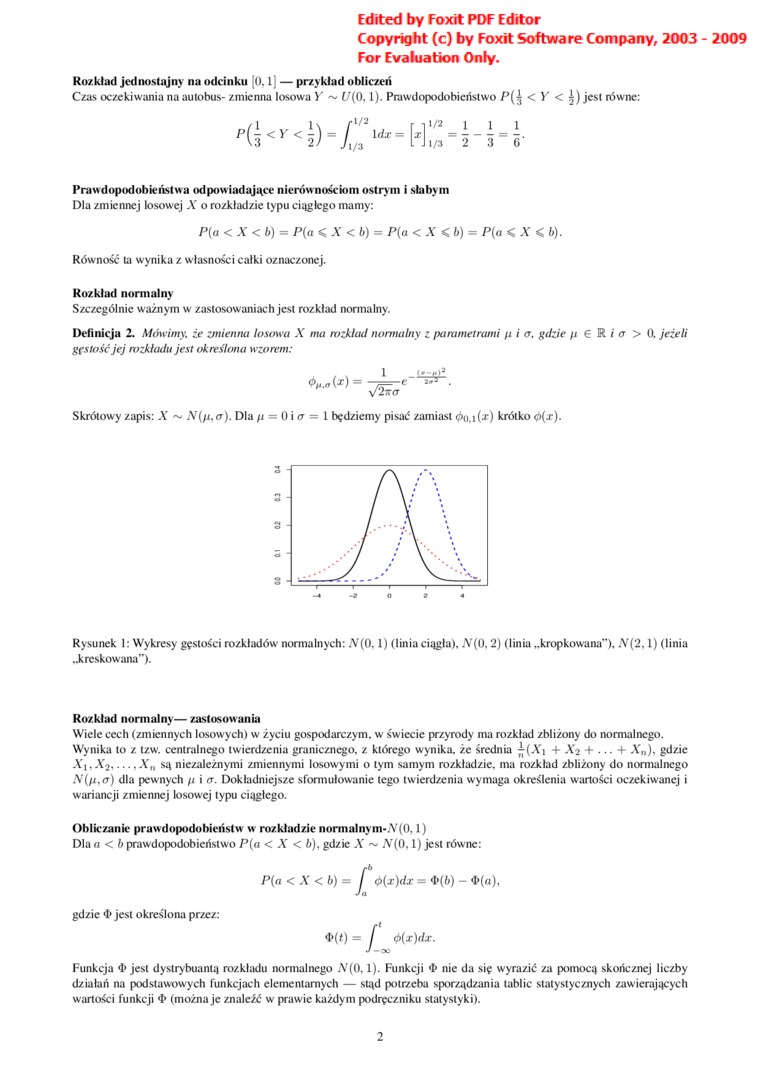
Rozkład normalny

Szczególnie ważnym w zastosowaniach jest rozkład normalny.

Definicja 2. Mówimy, że zmienno losowa X nui rozkład normalny z parametrami p i o, gdzie p € R i o > 0. jeżeli gęstość jej rozkłada jest okreśUma wzorem:

Skrótowy zapis: A' ~ N(p,<r). Dla p = 0 i o — 1 będziemy pisać zamiast ^o.i(-r) krótko <t>(x).

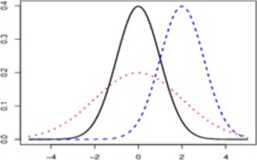
Rysunek 1: Wykresy gęstości rozkładów normalnych: JV(0,1) (linia ciągła), jV(0, 2) (linia „kropkowana"), .Y(2, ł) (linia ..kreskowana”).

Rozkład normalny— zastosowania

Wiele cech (zmiennych losowych) w życiu gospodarczym, w święcie przyrody ma rozkład zbliżony do normalnego. Wynika to z tzw. centralnego twierdzenia granicznego, z którego wynika, że średnia £(Ai + A2 + ... + X„), gdzie Ai. X₂,.... A„ są niezależnymi zmiennymi losowymi o tym samym rozkładzie, ma rozkład zbliżony do normalnego N(p.a) dla pewnych p i o. Dokładniejsze sformułowanie tego twierdzenia wymaga określenia wartości oczekiwanej i wariancji zmiennej losowej typu ciągłego.

Obliczanie prawdopodobieństw w rozkładzie normalnym-.V(0,1)

Dla a < b prawdopodobieństwo P(a < X < b). gdzie A ~ N(0.1) jest równe:

P(a < X <

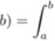
Ć>(x)dx = «I»(6) — ^(a).

gdzie 4> jest określona przez:

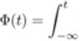
<t>{x)dx.

Funkcja 4> jest dystrybuantą rozkładu normalnego .V(0,1). Funkcji <l> nie da się wyrazić za pomocą skończnej liczby działań na podstawowych funkcjach elementarnych — stąd potrzeba sporządzania tablic statystycznych zawierających wartości funkcji (można je znaleźć w prawic każdym podręczniku statystyki).

2