34687

Rozkład jednostajny na odcinku '0,1 — przykład obliczeń

Czas oczekiwania na autobus- zmienna losowa Y ~ {/(O,1). Prawdopodobieństwo P(^ <Y < ^) jest równe:

^1/2 - i _ i - I

’^r| 1/3 ^— 2    3 ~ 6‘

Prawdopodobieństwa od pow jadające nierównościom osin m i słabym

Dla zmiennej losowej X o rozkładzie typu ciągłego mamy:

P(a < X < 6) = P(a < X < b) = P(a < X < b) = P{a < X < b).

Równość ta wynika z własności całki oznaczonej.

Rozkład normalny

Szczególnie ważnym w zastosowaniach jest rozkład normalny.

Definicja 2. Mówimy, że zmienna losowa X ma rozkład normalny z parametrami p i o, gdzie p € R i o > 0. jeżeli gęstość jej rozkładu jest określona wzorem:

Skrótowy zapis: A' ~ N(p,<r). Dla p = 0 i a = 1 będziemy pisać zamiast ^o.i(-r) krótko <t>(x).

-• -a o a 4

s 2 2 O 2

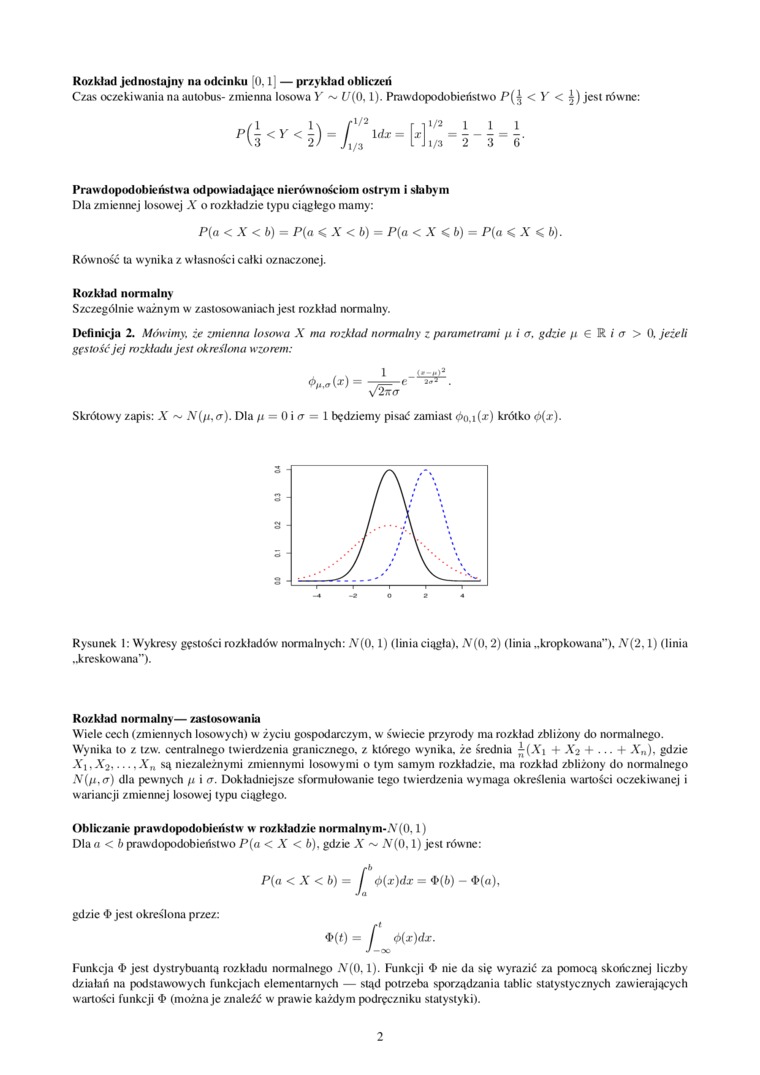
Rysunek 1: Wykresy gęstości rozkładów normalnych: JV(0,1) (linia ciągła), jV(0, 2) (linia „kropkowana"), .Y(2, ł) (linia ..kreskowana”).

Rozkład normalny— zastosowania

Wiele cech (zmiennych losowych) w życiu gospodarczym, w święcie przyrody ma rozkład zbliżony do normalnego. Wynika to z tzw. centralnego twierdzenia granicznego, z którego wynika, że średnia £(Xi + X^ + ... + X„), gdzie Ai. X₂,... ,X„ są niezależnymi zmiennymi losowymi o tym samym rozkładzie, ma rozkład zbliżony do normalnego N(p,a) dla pewnych p i o. Dokładniejsze sformułowanie tego twierdzenia wymaga określenia wartości oczekiwanej i wariancji zmiennej losowej typu ciągłego.

Obliczanie prawdopodobieństw w rozkładzie normalnym-.V(0,1)

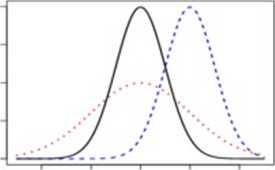
Dla a < b prawdopodobieństwo P(a < X < b). gdzie A ~ N(0.1) jest równe:

P(a< X <

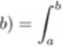
<f>(x)dx = ‘I*(6) — 4>(a),

gdzie 4> jest określona przez:

<t>(x)dx.

Funkcja 4> jest dystrybuantą rozkładu normalnego .V(0,1). Funkcji <I> nie da się wyrazić za pomocą skończnej liczby działań na podstawowych funkcjach elementarnych — stąd potrzeba sporządzania tablic statystycznych zawierających wartości funkcji (można je znaleźć w prawic każdym podręczniku statystyki).

2