5466967413

225.    Zmienne losowe Xi,X2,-. sa niezależne i mają wspólny rozkład jednostajny na odcinku (—1,1). Wykazać, że X\ ■ X2 ■ ■ ■ X_n dąży do zera prawie na pewno.

226.    Zmienne losowe X\,X2,-- sa niezależne i mają wspólny rozkład taki, że P(X_n = 1) = 3/4, P(F_n = —1) — 1/4. Wykazać, że X\ + ... + X_n zbiega do +oo prawie na pewno.

227.    Zmienne losowe X\, X2,... sa niezależne i mają wspólny rozkład wykładniczy z parametrem 3. Wykazać, że ciąg zmiennych losowych

X\ + ... + X_n + 3 n Xf + ... + X%

jest zbieżny prawie na pewno i wyznaczyć jego granicę.

228.    Niech X\,..., X_n będą niezależnymi zmiennymi losowymi o jednakowym rozkładzie z dys-trybuantą F, zaś F_n(t) — -^#{i < n: Xi < t} oznacza dystrybuantę empiryczną. Obliczyć EF„(x), VarF_n(x), Cov(F_n(x),F_n(y)).

229.    Niech X\,..., X_n będą niezależnymi zmiennymi losowymi o jednakowym rozkładzie z dys-

trybuantą F, zaś F_n(t) =    < n: Xi < t} oznacza dystrybuantę empiryczną. Pokazać, że

ciąg zmiennych losowych \/n(F_n(x) — F(x)) jest zbieżny do rozkładu normalnego. Zidentyfikować parametry tego rozkładu.

230.    Niech X\,..., X_n będzie próbką z rozkładu o dystrybuancie F, zaś X\_in < X2_:n < • • • < X_n:n będą statystykami porządkowymi (pozycyjnymi). Wykazać, że zmienna losowa Xk_:n ma dystrybuantę

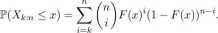
231.    Mamy trzy skrzynie, każda napełniona towarem pochodzącym z jednej z trzech fabryk. Wiemy, ze pierwsza fabryka wypuszcza 6% wadliwych towarów, druga 10%, a trzecia 4%. Losowo wybieramy jedną ze skrzyń (z jednakowym prawdopodobieństwem 1/3), a następnie losowo wybieramy jedną sztukę towaru.

a)    Jakie jest prawdopodobieństwo tego, że wylosujemy produkt wadliwy?

b)    Widzimy, że wybrana losowo sztuka towaru jest wadliwa. Jakie jest prawdopodobieństwo tego, że pochodzi z pierwszej fabryki?

c)    Widzimy, że wybrana losowo sztuka towaru jest wadliwa. Odkładamy ją do skrzyni i losujemy drugi raz, wciąż z tej samej skrzyni. Jakie jest prawdopodobieństwo tego, że za drugim razem wylosujemy produkt wadliwy?

232.    Samoloty bombowe przedzierają się przez dwie linie obrony przeciwlotniczej. Każdy samolot, niezależnie od pozostałych, z prawdopodobieństwem 9 może zostać strącony przez pierwszą linię obrony. Jeśli pokona pierwszą linię, z prawdopodobieństwem 9 może zostać strącony przez drugą linię. Prawdopodobieństwo 9 jest nieznane. Spośród n = 100 samolotów, Ki — 40 zostało strąconych przez pierwszą linię, a dalszych K2 = 20 zostało strąconych przez drugą linię.

a)    Obliczyć wiarogodność dla zaobserwowanych wartości K\ i K2, czyli Po (Fi = 40, F₂ = 20).

b)    Podać estymator największej wiarogodności parametru 9.

233.    Niech Xi,..., X_n będzie próbką z rozkładu normalnego N(0, a²) (o wartości oczekiwanej równej 0 i nieznanej wariancji).

a)    Podać wzór na estymator a największej wiarogodności parametru er, czyli odchylenia standardowego.

b)    Obliczyć wartość oczekiwaną i wariancję o².

234.    Wykonujemy n = 8 doświadczeń zgodnie ze schematem Bernoulliego, z nieznanym prawdopodobieństwem 9 sukcesu. Niech K będzie liczbą sukcesów. Rozważamy dwa estymatory:

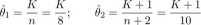
17