123153

OY

O

OX

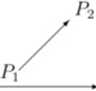
Punkt P\ nazywamy początkiem wektora, a punkt P₂ końcem. Odległość \P\P2\ nazywamy długością wektora. Wektor PP nazywamy wektorem zerowym. Każdą prostą równoległą do wektora P\ P₂ nazywamy kierunkiem tego wektora. Wektory nazywamy równoległymi (kolinearnymi) jeśli mają równoległe kierunki. Mówimy, że dwa wektory kolinearne P\ P>. P.\P\ mają taki sam zwrot gdy odcinki P\P\. P2P3 mają punkt wspólny w przeciwmym razie mówimy, że wektory mają zwrot przeciwny.

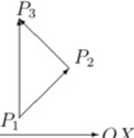
Dla dowolnych punktów Pj, P₂. P3 wektor P1P3 nazywamy sumą wektorów P\ P₂. P2P3 i piszemy:

P\P?. = P\p2 + P2P3

O)

O

Wektory PiP₂, P3P1 nazywamy równoważnymi, gdy mają taką samą długość, są kolinearne i mają ten sam zwrot. Będziemy takie wektory uważać za równe i nazywać je będziemy wektorami swobodnymi. Wektory swobod-ne będziemy oznaczać małymi literami alfabetu i czasem będziemy używać strzałek. Każdy wektor swobodny na płaszczyźnie utożsamiać będziemy z parą liczb rzeczywistych [x, y]. Jeśli Pi(xi,X2) jest początkiem wektora, a Pi{x2- IJ2) jego końcem to x = x₂ — X\,y = ys — y\. Dowolne dwa wektory swobodne można dodaw^rać i jeśli a = [z_a. y_a],b =    to:

a + b = [x_a + *6, Ifa' yb]

2