53289

Politechnika Świętokrzydui. Ryszard Florek

Rachunku Wyrównawczym a na razie przyjmujemy, źe wagi obserwacji mogą być przez nas ustalane arbitralnie (zgodnie z naszą intuicją) lub jako odwrotność kwadratu błędu średniego, czyli:

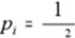
Wartości n giprawdop odobnieisr e niierronycli wielkości - średnia arytmetyczna i średnia wat ona Spostrzeżenia bezpośrednie o jednakowej dokładności Spostrzeżenia bezpośrednie o niejednakowej dokładności

°o

#»

Y x,

- średnia arytmetyczna n

OK =

l U - -*)²

\^r

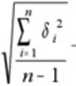
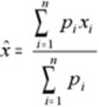
- średnia ważone (ogólna)

odchylenie

standardowe dla spostrzeżeń jednakowo dokładnych zwane również błędem pojedynczego pomiaru przed wyrównaniem (błąd średni)

\

n- 1

0 _x = m_x = -r= odchylenie standardowe średniej V//

arytmetycznej, (błąd średni średniej arytmetycznej), zwany też błędem po wyrównaniu

odchylenie standardowe dla spostrzeżeń niejednakowo dokładnych zwane również błędem pojedynczego pomiaru przed wyrównaniem (błąd średni)

0 . = nr =

n

Ip.

odchylenie standardowe średniej

W

Kontrola : £ 8, = 0

i*l

ogólnej, (błąd średni średniej ogólnej), zwany też błędem po wyrównaniu

II

Kontrola : £ pfi _t - 0

<«i

Metoda nqininieis~vch kwadratów

Pierwszą kompletną publikacją dotyczącą metody najmniejszych kwadratów była słynna Thcoria Motus Gaussa od tamtej pory metoda ta ciągle jest rozwijana i trudno o niej pisać yv kilku zdaniach dlatego ograniczymy się tutaj jedynie do podania jej głównej zasady. W metodzie tej chcemy tak zniekształcić wyniki pomiarów aby suma kwadratów odchyłek losowych 8 była jak najmniejsza, czyli:

n    n

£ &² -> min lub £ pfi ₍² -> min

i    i

Wyprowadzenie formuły na średnią ogólną za pomocą metody najmniejszej sumy kwadratów (MNK)

#1

£ /■>,<*/ -> min

I

Obserwujany pewną yviclkość u i otrzymujemy serię pomiarów Xi, x_:.....x. oczyyviścic za każdym razem mamy do czynienia

z błędami przypadkoyyymi, błędy przypadkowe w naszym modelu pomiaru „ukryte" są w składniku losowym 8, czyli możemy zapisać serię pomiarów jako:

AT, = U + 8, -» $, = X, - U

*2 = U + 5 2 S₂ ^s X₂- u x_H = u + 5 „ -» $ „ - x_n - u

Korzystając z zasady MNK otrzymujemy:

#»

£ pff = P|(.v, - m)² + p₂(x₂ ■ «)* + pS^x„ - w)² = /M -* min