7292100785

Rachunek wyrównawczy. 457

Rachunek wyrównawczy.

Napisał

Dr. Kasper Weigel,

profesor politechniki, Lwów.

Błedv mzypadkowc. Błąd średni. Wagi spostrzeżeń. Metoda najmniejszych kwadratów. Wyniki spostrzeżeń wielkości fizycznych, ehocb) najstaranniejsze, nie są bezbłędne; wymagaj,*} zastosowania rachunku wyrównawczego takiego, aby wyniki, otrzymane za jego pośrednictwem, mog y bvć uważane za na bardziej prawdopodobno. Zarazem chcemy znać do-ich błędów prawdopodobnych¹*, w praktyce z leguły „średniej .

nrubyjch (przeoczeń obserwatora) i systematycznych (tj. związanych ścisłe z okolicznościami towarzysząeemi pomiarom); mogą być zatem obarczone tv'kn błędami t zw. „przypadkowemi", tj. błędami, ktorjch przyczy y zależą od okoliczności, zmieniających się w

Rachunek wyrównawczy opiera się na rachunku prawdopodobieństwa. Błedv przypadkowe dzielimy na „prawdziwe i „pozorne .

Biorąc pod uwagę najprostszy rodzaj spostrzeżeń, t. zw. bezpośrednich, tj przeprowadzonych bezpośrednio nad pewną wielkością, której wartość prawdziwa niech bedzie X, otrzymamy na e, błąd prawdziwy, związek

e = X-l............. (ł)

przyczem l jest wartością, uzyskaną ze spostrzeżenia.

Natomiast wzór na błąd pozorny 3 opiewa w tym przypadku:

. .......(2)

przyczem x oznacza wartość spostrzeganej wielkości, uzyskaną przy pomocy rachunku wyrównawczego (wartość wyrównaną).

Analogicznie urobimy oba powyższe błędy w przypadku, gdy spostrzeżenia L są funkcjami pewnych wielkości stałych X, i , Z, . . . któ wartości najbardziej prawdopodobnych x, y, z, . . .

rachunek wyrównawczy, tj. w    przypadku spostrzeżeń t. zw. pośrednich, zatem •

z = f{X,Y,Z,    ,     (3)

—L.........(⁴)

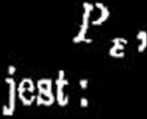
prawdopodobieństwo pojawienia się błędu z w szeregu spostrzeżeń,

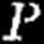
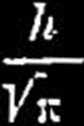
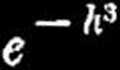
dt (prawo Gaussa)

przyczem h jest miarą dokładności spostrzeżeń. Z wzoru (4) widać, że prawo Gaussa określa prawdopodobieństwo P_£ jako funkcję parzystą ( ^

Wielkość h wzgl h~, można wyznaczyć dla dokonanego szeregu spos    ze stosunku ich ilości n do podwójnej sumy kwadratów ich błę

dów 2 ^v e² 2 [es] (sposób oznaczenia sum w ruch. wyrówn.), a mianowicie:

i

u

7,2___

2[eej

. (Ściśle dla n — oo)

(<*>)

Wprowadzając pojecie t. zw. „błędu średniego" ji, określonego wzorem (ściśle dla n = oc):

119

i* - ...    ......... <^?>