ZADANIE Z ĆWICZEŃ - zagadnienie transportowe

Przedsiębiorstwo posiadające 3 wytwórnie prefabrykatów betonowych wysyła swoje produkty do 3 hurtowni. Podaż wytwórni wynosi odpowiednio 20, 30, 20 ton, natomiast popyt hurtowni 25, 28, 17 ton. Jednostkowe koszty transportu przedstawia tabela poniżej. Wyznacz optymalny plan dostaw, minimalizując całkowity koszt transportu. Podaj wielkość optymalnego kosztu.

	H1 25t	H2 28t	H3 17t
W1 20t	2	5	4
W2 30t	1	3	6
W3 20t	2	2	7

Wartości w tej tabeli oznaczają, że np. koszt przewiezienia tony towaru od wytwórcy W1 do hurtowni H1 wynosi 2 zł.

1. Musimy sprawdzić czy zadanie jest zbilansowane - czyli czy popyt równa się podaży

Popyt hurtowni=25+28+17=70

Podaż wytwórni=20+30+20=70

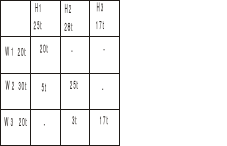
2. Wyznaczamy pierwsze rozwiązanie dopuszczalne

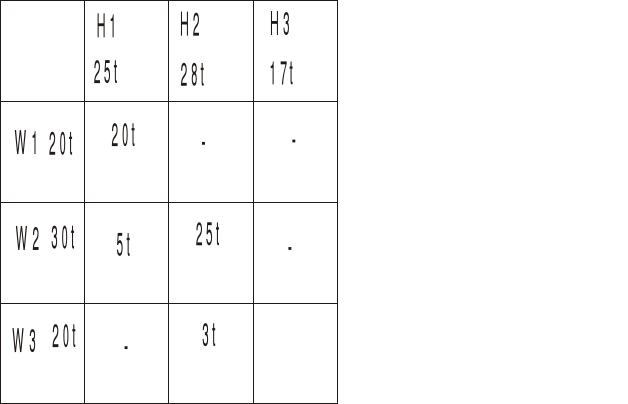
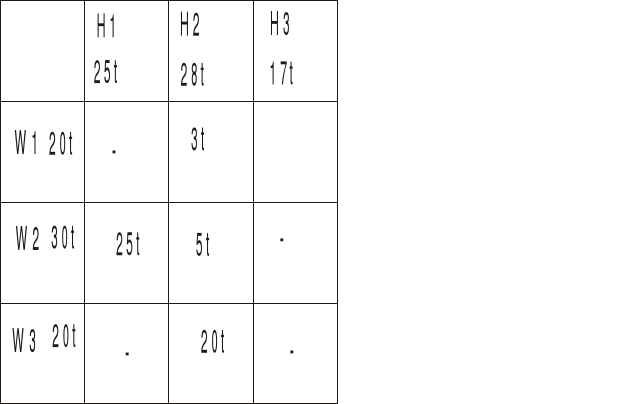
1. najpierw metodą kąta północno-zachodniego (nazwa stąd, że zaczynamy od lewego, górnego prostokąta - tego czerwonego)

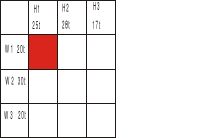
Do tego kwadratu wpisujemy jak najwięcej towaru, w naszym przypadku to będzie 20t, bo dostawca W1 więcej już nie ma.

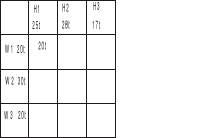
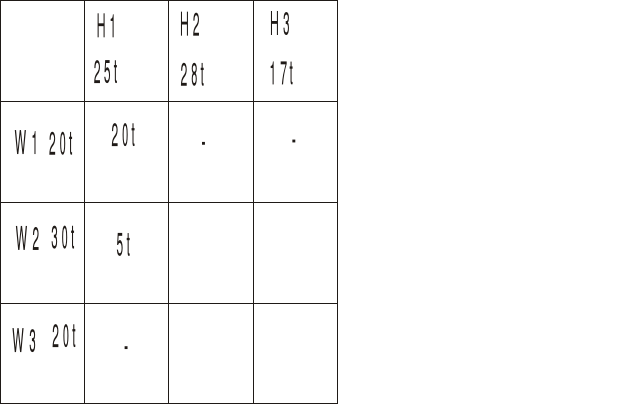
Ponieważ hurtownia H1 potrzebuje 25t a od W1 dostała tylko 20t, to brakujące 5t bierzemy od kolejnego dostawcy W2.

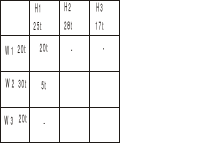
Jak widać dostawca W1 dał całość do H1 i do H2 i H3 już nic nie dostarczy. Hurtownia H1 wzięła od W1 20t i od W2 5t czyli więcej już nie potrzebuje i nic nie weźmie od W3.

Ponieważ dostawcy W2 zostało 25t więc kierujemy je do kolejnej hurtowni H2 i upychamy jak najwięcej. H2 potrzebuje 28t, więc weźmie całe 25t od W2 i jeszcze dobierze 3t od W3.

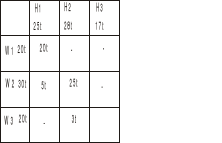
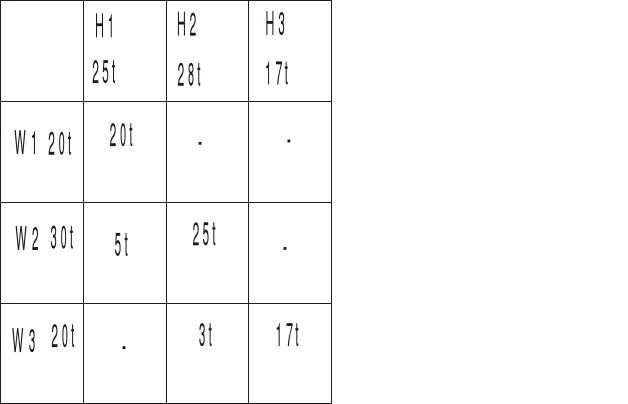
Jak widać dostawcy W1 i W2 już nic nie mają a hurtownie H1 i H2 już nic nie potrzebują, to co zostało u dostawcy W3 idzie do H3

2. metoda minimalnego kosztu

W tabeli kosztów szukamy kosztu najmniejszego

	H1	H2	H3
W1	2	5	4
W2	1	3	6
W3	2	2	7

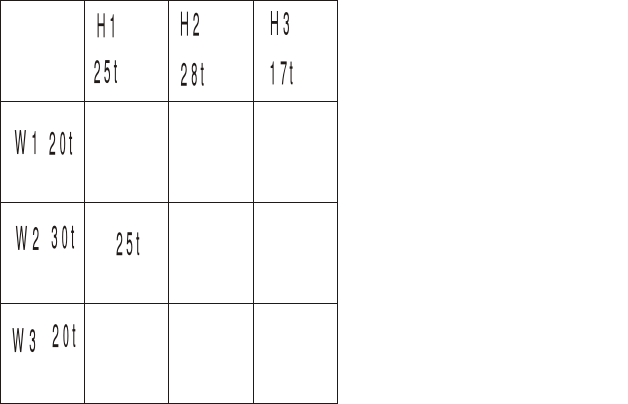
Od tego kwadratu zaczynamy dostawy

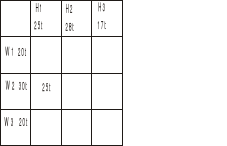
Dajemy maksymalnie tyle, ile się zmieści - hurtownia H1 chce 25t a W2 może dostarczyć tyle, więc wpisujemy 25t, H1 nie weźmie już nic od W1 i W2

Patrzymy, gdzie teraz jest najniższy koszt (nie biorąc już pod uwagę kolumny H1

	H1	H2	H3
W1	2	5	4
W2	1	3	6
W3	2	2	7

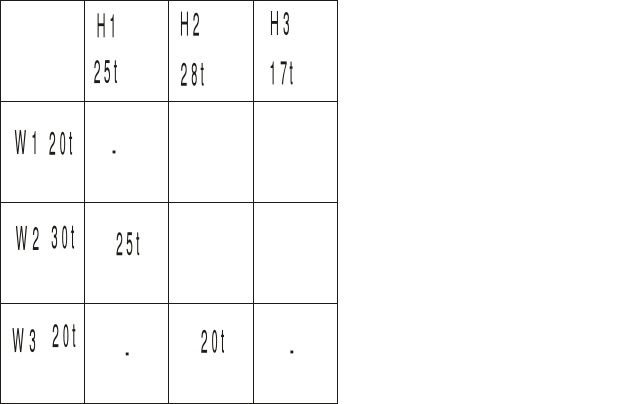
i tu wpisujemy jak najwięcej - H2 potrzebuje 28t a W3 może dostarczyć 20t stąd wpisujemy 20t i od W3 nic już nie pójdzie do H3

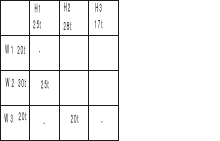
Teraz w kolumnie kosztów H2 patrzymy od którego z pozostałych dostawców H2 może dostać taniej

	H1	H2	H3
W1	2	5	4
W2	1	3	6
W3	2	2	7

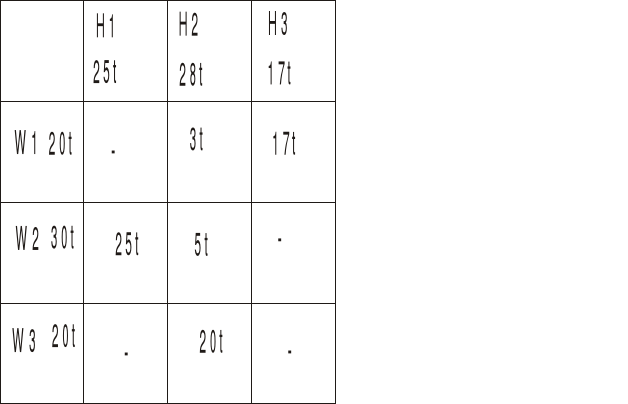
Taniej będzie od W2 więc od niego bierzemy ile się da. A dostawca W2 dostarczył już 25t do H1 i zostało mu do dyspozycji tylko 5t, bierzemy te 5t, co razem z 20 tonami od W3 daje nam dostawę do H2=25t. A H2 ma zapotrzebowanie w sumie na 28t, brakujące 3t bierzemy od W1 (bo tylko on został)

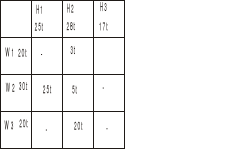
Został nam dostawca W1 z 17 tonami i odbiorca H3, który na nie czeka - wpisujemy te 17t

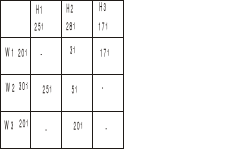
3. Wyznaczamy funkcje celu dla rozwiązań

FC to wartość kosztów transportu (czyli suma iloczynów kosztu jednostkowego i ilości dostaw) - mnożymy wartości z tych samych komórek macierzy kosztów i macierzy dostaw.

dla met. a)

FC=20t*2zł+5t*1zł+25t*3zł+3t*2zł+17t*7zł=245zł

dla met. b)

FC=25*1+3*5+5*3+20*2+17*4=163 zł

4. Sprawdzamy czy rozwiązanie jest optymalne (dla met. minimalnego kosztu)

Aby sprawdzić optymalność rozwiązania

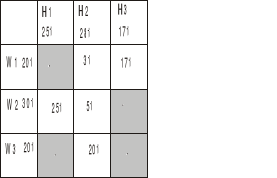
	H1	H2	H3
W1	2	5	4
W2	1	3	6
W3	2	2	7

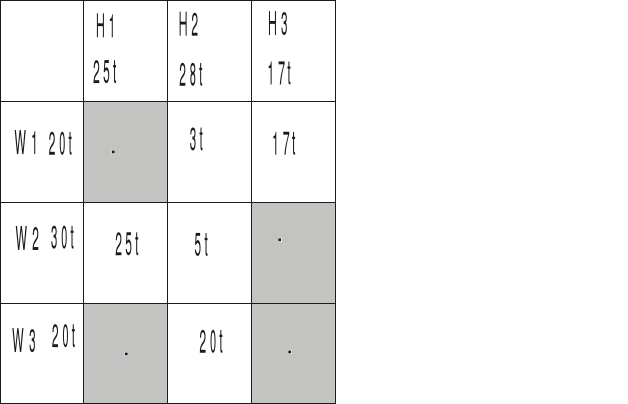
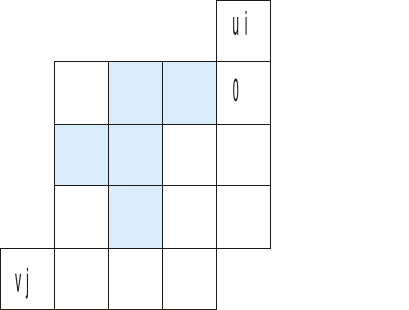
skupiamy się tylko na polach gdzie są wpisane wartości przewozów (tych białych, te szare nas nie interesują)

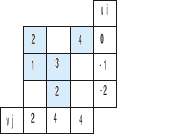
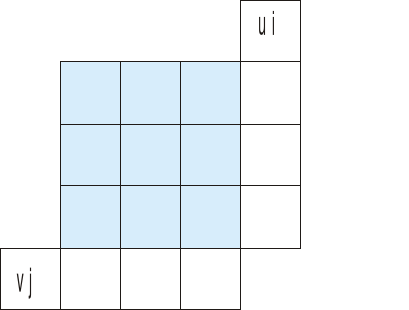
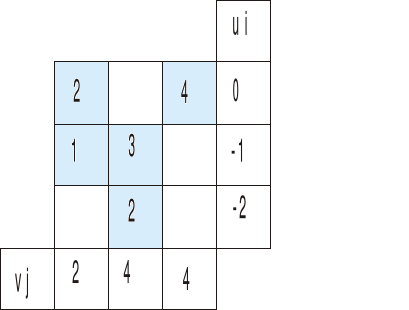
Po pierwsze musimy wyznaczyć potencjały ui oraz vj

według wzoru cij=ui+vj gdzie cij to pola (te niebieskie) w macierzy poniżej

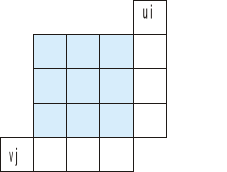
Zaczynamy zawsze od wpisania zera w pozycji u1

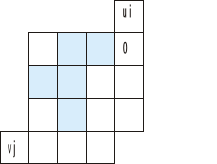
Interesują nas tylko pola przewozów (te niebieskie), wpisujemy w nie odpowiednie koszty z tabeli kosztów jednostkowych.

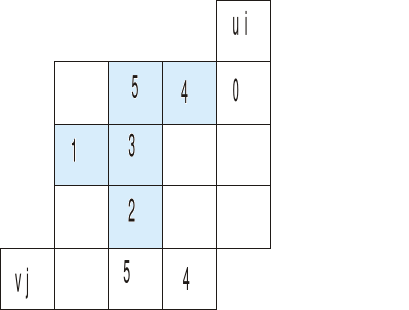
Ponieważ w 3 kolumnie 4 to jedyne niebieskie pole więc tą 4 przepisujemy też w rząd vj (jak widać powyżej)

Dlaczego? bo ze wzoru cij=ui+vj wynika:

4=0+vj

vj=4

A teraz patrzymy na 5 w pierwszym rzędzie i na wzór

5=0+vj stąd

vj=5

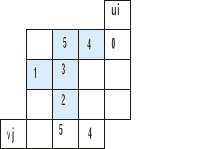
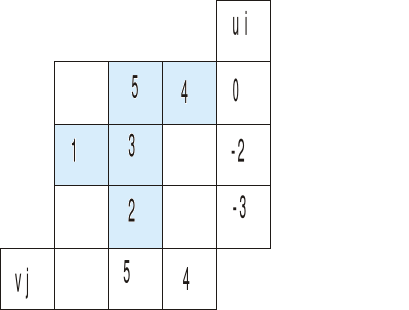
mając vj=5 patrzymy na rząd trzeci:

2=ui+5

ui=-3

i na rząd drugi

3=ui+5

ui=-2

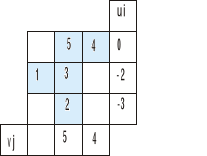
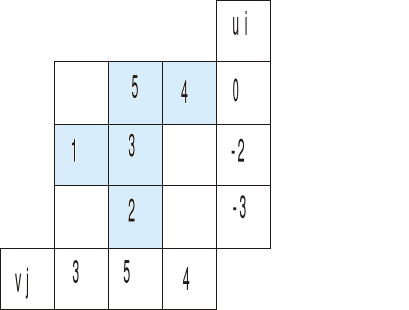
I zostało nam do wyznaczenia vj w pierwszej kolumnie

1=-2+vj

vj=3

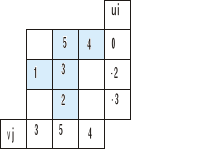
Budujemy macierz kosztów zredukowanych wg wzoru C^Bij=cij-ui-vj

Liczymy C^Bij dla wszystkich komórek macierzy kosztów

	H1	H2	H3
W1	2	5	4
W2	1	3	6
W3	2	2	7

Czyli od lewego górnego rogu:

-1	0	0
0	0	4
2	0	6

2-0-3=-1 5-0-5=0 4-0-4=0

1-(-2)-3=0 3-(-2)-5=0 6-(-2)-4=4

2-(-3)-3=2 2-(-3)-5=0 7-(-3)-4=6

Czyli macierz:

Tam gdzie są przewozy w macierzy C^Bij będą zera. Rozwiązanie jest optymalne gdy w tej macierzy nie ma liczb mniejszych od zera. W naszej macierzy jest taka liczba tzn. -1

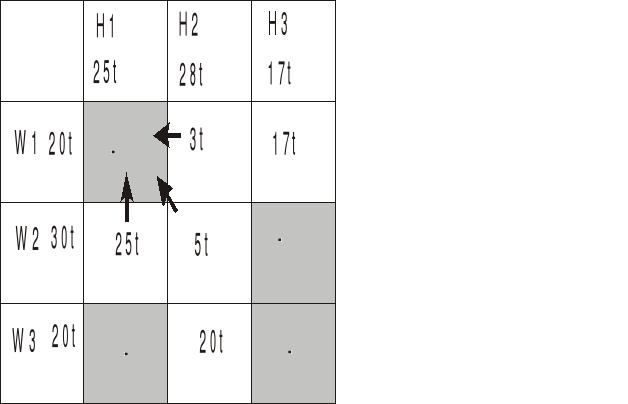
Oznacza to, że biorąc macierz z planem transportowym, staramy się przesunąć jak najwięcej towaru na pole, które odpowiada polu z liczbą -1 w macierzy kosztów zredukowanych (w naszym zadaniu jest to pole lewe górne). Przesuwać możemy z pól sąsiednich.

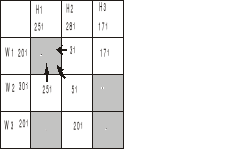
Te przesunięcia trzeba robić tak aby zbilansować dostawców i odbiorców.

Jeśli, np. przesuniemy 25t z pola W2H1 to nie zbilansujemy bo W1 może dostarczyć tylko 20t. Można by przesunąć tylko 20t ale wtedy byłoby te 20t na polu W1H1 a W1 może dostarczyć tylko 20t, więc trzeba by zabrać 3 i 17t z pól W1H2 i W1H3.

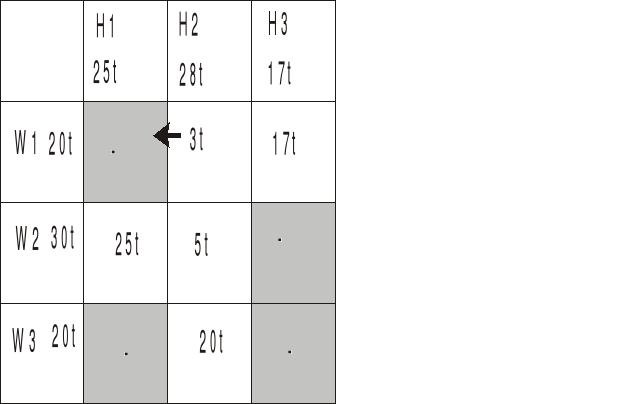
Jeśli przesuniemy 5t z W2H2 ale W2 ma do dostarczenia 30t a H2 musi dostać 28t

Ale jeżeli przesuniemy 3t z W1H2 na W1H1

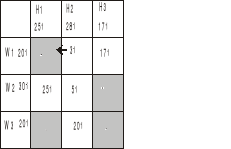
To mamy taką sytuację

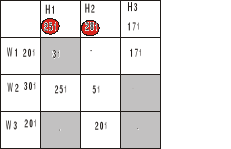
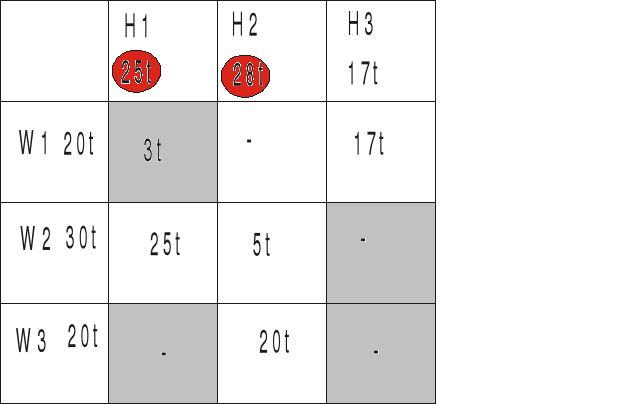
Nie zgadzają nam się wartości dla H1 i H2

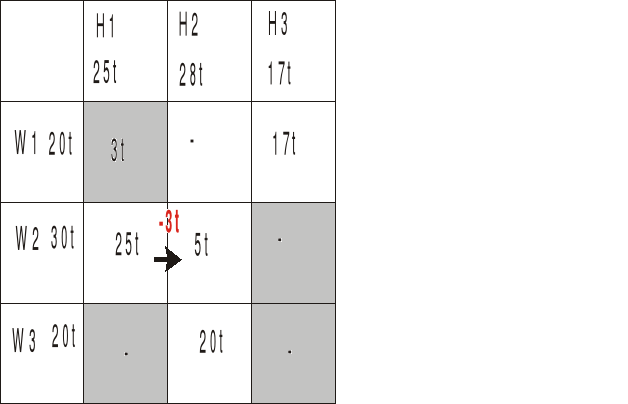
Przesuwamy więc z W2H1 tyle aby H1 dostał swoje 25t a H2 swoje 28t

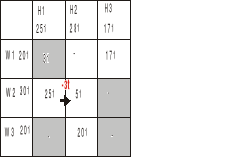
I sytuacja jest taka, że wszystko się bilansuje

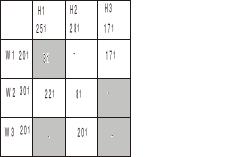
Wyznaczamy potencjały ui oraz vj metodą jw.

Budujemy macierz kosztów zredukowanych wg wzoru C^Bij=cij-ui-vj

0	1	0
0	0	3
2	0	5

Jest to rozwiązanie optymalne (nie ma liczb ujemnych)

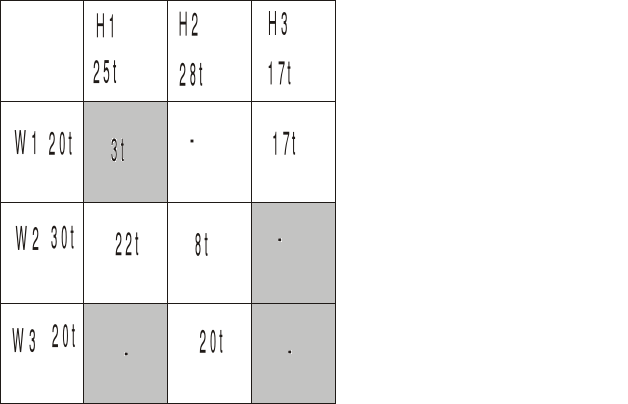
Optymalny plan przewozów:

	H1 25t	H2 28t	H3 17t
W1 20t	3t	-	17t
W2 30t	22t	8t	-
W3 20t	-	20t	-

Wartość funkcji celu dla rozwiązania optymalnego wynosi:

FC = 3*2 + 22*1 + 8*3 +20*2+ 17*4 = 160 zł

1

---