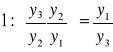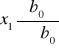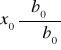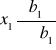Pojęcie i rodzaje szeregów czasowych
Analizę dynamiki zjawisk masowych przeprowadza się na podstawie szeregów czasowych (inaczej dynamicznych, chronologicznych).
Szeregiem dynamicznym nazywamy ciąg wartości badanego zjawiska obserwowanego w kolejnych jednostkach czasu.
W szeregach czasowych zmienną niezależną jest czas, natomiast zmienną zależną - wartości liczbowe badanego zjawiska:
![]()
Gdzie: yt - zmienna zależna; t - zmienna niezależna (czas); f - określona funkcja matematyczna.
Zmienna niezależna w szeregach czasowych może być ujmowana różnie, w zależności od celu badania i właściwości zjawisk masowych. Zjawiska zmieniające się wolno są ujmowane w pewnych ściśle określonych momentach, np. według stanu w dniu lub godzinie. Szeregi zbudowane w ten sposób noszą nazwę szeregów czasowych momentów (np. liczba ludności Polski na dzień 31 XII w kolejnych latach). Szeregi czasowe zawierające informacje o rozmiarach zjawiska w pewnych - dłuższych lub krótszych - okresach (np. półrocze, kwartał) nazywamy szeregami czasowymi okresów. Przykładem takiego szeregu jest np. szereg przedstawiający wielkość produkcji w przedsiębiorstwie w kolejnych miesiącach określonego roku.
Przeciętny poziom zjawisk przedstawionych w postaci szeregów czasowych okresów - przy założeniu, że przyjęte przedziały czasowe są równe - oblicza się za pomocą średniej arytmetycznej.
Do obliczania średniego poziomu zjawisk przedstawionych w formie szeregów czasowych momentów wykorzystuje się średnią chronologiczną. Oblicza się ją wg wzoru:
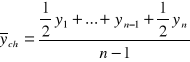
gdzie: y1, y2, …, yn oznaczają wielkość badanego zjawiska w kolejnych momentach.
Rozwój zjawisk przedstawiony za pomocą szeregów czasowych może być właściwie oceniony wówczas, gdy poszczególne wyrazy szeregów czasowych są wielkościami jednorodnymi i porównywalnymi.
Porównywalność danych statystycznych przedstawionych w formie szeregów czasowych jest możliwa, gdy spełnione są określone warunki:
Zjawiska przedstawione w szeregach czasowych powinny być wyrażone w tych samych jednostkach miar; badając np. poziom spożycia alkoholu w pewnym okresie można porównać ilość alkoholu sprzedawanego konsumentom bez względu na zawartość czystego alkoholu bądź też po przeliczeniu na czysty alkohol.
Szeregi czasowe okresów mogą być porównywane z szeregami czasowymi okresów, a szeregi czasowe momentów z szeregami czasowymi momentów, przy czym muszą one dotyczyć tych samych momentów lub okresów; nie można np. porównywać liczby ludności w Polsce w dniu 31 XII 2001 r. z liczba ludności Węgier w dniu 30 VI 2001 r.
Badane w czasie zjawiska powinny dotyczyć tego samego obszaru terytorialnego; nie można porównywać liczby ludności województwa warszawskiego z dnia 30 VI 1970 r. z liczbą ludności tego województwa z dnia 30 VI 1980 r., ponieważ dnia 1 VI 1975 r. nastąpiła zmiana podziału administracyjnego kraju.
W szeregach dynamicznych okresów przedziały czasowe powinny być jednakowe; problem ten jest szczególnie istotny przy porównywaniu szeregów, w których jednostkami czasu są miesiące lub kwartały - sprawdzenia wartości zjawisk do okresów porównywalnych (np. zawierających jednakową liczbę dni) dokonuje się wg wzoru:
![]()
gdzie: yto - wielkość obserwowanego zjawiska przy założeniu, że wszystkie jednostki czasu (np. miesiące, kwartały) mają jednakową liczbę dni; yt - faktycznie zaobserwowane wielkości zjawiska w danej jednostce czasu; to - liczba dni w danej jednostce czasu przyjęta za podstawę porównywalności (np. 30 dni dla miesięcy, 91 dni dla kwartałów), z - rzeczywista liczba dni kalendarzowych w danej jednostce czasu.
Proste metody badania zmian szeregu dynamicznego
Dwie liczby można ze sobą porównać
przez odejmowanie lub dzielenie.
Przyrosty absolutne
Odejmowanie dwóch wielkości liczbowych daje w wyniku dodatni lub ujemny przyrost absolutny (bezwzględny).
Przyrosty absolutne mogą być obliczane w stosunku do jednego okresu (momentu) przyrosty absolutne o podstawie stałej (jednopodstawowe) lub też okresu (momentu) stale zmieniającego się przyrosty absolutne o podstawie zmiennej (łańcuchowe).
Jeżeli poszczególne wyrazy szeregu dynamicznego oznaczymy przez: y1, y2, …, yn i za podstawę porównań przyjmiemy wielkość y1, to ciąg przyrostów absolutnych o podstawie stałej przedstawia się następująco:
![]()
Natomiast ciąg przyrostów absolutnych łańcuchowych ma postać:
![]()
Jak wynika z powyższego przyrosty absolutne informują o tym, o ile jednostek wzrósł (znak plus) lub zmalał (znak minus) poziom badanego zjawiska w okresie (momencie badanym w porównaniu z okresem (momentem) przyjętym za podstawę.
Przyrosty absolutne są wielkościami mianowanymi, wyrażonymi w tych samych jednostkach miary, co badane zjawiska. Wynika z tego, że nie nadają się one do porównań ze zmianami innych zjawisk, które są wyrażone w odmiennych jednostkach miary lub, których rząd wielkości jest inny.
Przy obliczaniu przyrostów absolutnych bardzo ważny jest wybór podstawy porównań. Wybrany do porównań okres powinien być na tyle charakterystyczny, aby pozwalał poznać istotę zachodzących zmian. Dlatego też nie należy przyjmować za podstawę okresu zupełnie wyjątkowego pod względem poziomu badanego zjawiska, gdyż wszystkie porównania byłyby wówczas zniekształcone. Np. badając poziom produkcji żelaza w Chinach po II wojnie światowej należy pamiętać, że w wyniku „Wielkiego Skoku” produkcja w wielkościach bezwzględnych gwałtownie wzrosła w krótkim okresie czasu, aby później równie gwałtownie zmaleć. Przyjmując więc za podstawę okres (moment) tuż sprzed „Wielkiego Skoku” uzyskamy niespotykanie korzystny obraz produkcji żelaza w Chinach. Analogicznie przyjmując za podstawę okres (moment z) „Wielkiego Skoku” uzyskamy skrajnie niekorzystny obraz tejże produkcji.
Przyrosty względne;
Przyrostem względnym nazywamy iloraz (dla niewtajemniczonych wynik dzielenia) przyrostów absolutnych zjawiska do jego poziomu w okresie (momencie) przyjętym za podstawę do porównań.
Przyrosty względne podobnie jak absolutne mogą być jednopodstawowe lub łańcuchowe.
Ciąg wartości przyrostów względnych o stałej podstawie y1, wygląda następująco:
![]()
Z powyższego wynika, że przyrost względnych łańcuchowych wygląda następująco:
![]()
Przyrosty względne najczęściej wyrażane są w procentach.
Informują o tym, o ile wyższy lub niższy jest poziom badanego zjawiska w danym okresie w stosunku do okresu bezpośrednio poprzedzającego (przyrosty względne łańcuchowe) lub w porównaniu z okresem przyjętym za podstawę (przyrosty względne jednopodstawowe).
Przyrosty względne mogą być wartościami dodatnimi, ujemnymi lub równymi zero.
Przyrosty względne określane są mianem wskaźników tempa wzrostu.
Wskaźniki dynamiki (indeksy)
Indeksem (wskaźnikiem dynamiki) nazywamy każdą liczbę względną powstałą przez podzielenie wielkości danego zjawiska w okresie badanym (sprawozdawczym) przez wielkość tego zjawiska w okresie podstawowym (bazowym).
Jeżeli poziom zjawiska w okresie (momencie) badanym oznaczamy symbolem y1, a w okresie (momencie) podstawowym symbolem y0 to wzór na indeks przyjmuje postać:
![]()
Indeks jest wielkością niemianowaną i może być wyrażony w ułamkach lub w procentach.
Jeżeli indeks przyjmuje wartość z przedziału 0 < i < 1, to świadczy to o spadku poziomu zjawiska w badanym okresie w stosunku do okresu podstawowego. Wartość większa od 1 (lub 100%) świadczy o wzroście poziomu zjawiska w okresie badanym w stosunku do okresu podstawowego. Wartość indeksu równa 1 świadczy o tym, że poziom zjawiska w okresach badanym i podstawowym są takie same.
W zależności od przyjętej podstawy wyróżniamy indeksy jednopodstawowe lub łańcuchowe.
Ciąg indeksów o podstawie stałej zapisujemy następująco:
![]()
Ciąg indeksów łańcuchowym (oparty na zasadzie odnoszenia poziomu badanego zjawiska z okresu badanego do poziomu tego zjawiska w z okresu bezpośrednio poprzedzającego) zapisujemy następująco:
![]()
Technika obliczania przyrostów absolutnych, względnych oraz indeksów
Obliczanie przyrostów absolutnych, względnych oraz indeksów na podstawie danych dotyczących rozwodów w Polsce w latach 1970 - 1977.
Lata |
Rozwody ( w tys.) |
Przyrosty absolutne |
Przyrosty względne |
Indeksy |
|||
|
|
Jedno-podstawowe (1970 = 100) |
Łańcuchowe |
Jedno-podstawowe (1970 = 100) |
Łańcuchowe |
Jedno-podstawowe (1970 = 100) |
Łańcuchowe |
1970 1971 1972 1973 1974 1975 1976 1977 |
34,6 36,3 37,4 39,7 39,7 41,3 38,0 43,2 |
0,0 1,7 2,8 5,1 5,1 6,7 3,4 8,6 |
- 1,7 1,1 2,3 0,0 1,6 -3,3 5,2 |
0,0 4,9 8,1 14,7 14,7 19,4 9,8 24,9 |
- 4,9 3,0 6,1 0,0 4,0 - 8,0 13,7 |
100,0 104,9 108,1 114,7 114,7 119,4 109,8 124,9 |
- 104,9 103,0 106,1 100,0 104,0 92,0 113,7 |
Źródło: M. Sobczyk, Statystyka, W-wa 1991, s. 274.
Jak widać z powyższego między przyrostami względnymi a indeksami zachodzi ścisły związek.
Indeksy jednopodstawowe można otrzymać z przyrostów względnych o podstawie stałej przez dodanie 100 (lub 1, jeżeli posługujemy się ułamkami, a nie wielkościami procentowymi). W analogiczny sposób można dokonać przeliczenia indeksów łańcuchowych na przyrosty względne łańcuchowe. Na tej samej zasadzie można dokonać operacji odwrotnej, tzn. zmienić indeksy łańcuchowe (lub jednopodstawowe) na przyrosty względne łańcuchowe (lub jednopodstawowe). Wielkość przyrostu względnego jest wówczas wielkością odpowiedniego indeksu pomniejszoną o 100 (lub 1).
W praktyce badań statystycznych najczęściej wykorzystuje się indeksy. Są one bowiem wygodnym materiałem dla dalszych badań i działań matematycznych. Działania, jakie można na nich wykonać sprowadzają się w zasadzie do zamiany indeksów jednopodstawowych na łańcuchowe i odwrotnie oraz do zamiany podstawy w szeregu indeksów o podstawie stałej.
Zamiany indeksów jednopodstawowych na łańcuchowe dokonujemy poprzez dzielenie indeksów jednopodstawowych przez siebie, zgodnie ze wzorem:
![]()
Zamiany indeksów łańcuchowych na jednopodstawowe dokonujemy według następujących zasad:
Indeks jednopodstawowy w okresie następującym bezpośrednio po okresie przyjętym za podstawę jest taki sam jak indeks łańcuchowy.
Indeks jednopodstawowy w okresie przyjętym za podstawę wynosi 100%.
Dalsze indeksy jednopodstawowe po okresie przyjętym za podstawę otrzymujemy mnożąc w sposób narastający (kumulując) kolejne indeksy łańcuchowe, licząc od wskaźnika łańcuchowego znajdującego się tuż po okresie podstawowym.
Indeksy jednopodstawowe przed okresem podstawowym są odwrotnością narastających iloczynów kolejnych indeksów łańcuchowych, licząc od okresu przyjętego za podstawę.
Zmiany podstawy w indeksach jednopodstawowych dokonujemy przez dzielenie poszczególnych indeksów przy danej podstawie przez indeks jednopodstawowy tego okresu, który przyjmujemy za nową podstawę.
Operacje na szeregach indeksowych przedstawia tabela:
Operacje w tabeli są wykonane dla t = 3, w ten sam sposób można je wykonać dla każdej innej wartości t dla dowolnego szeregu dynamicznego.
t |
Absolutny (yt) |
Indeksy |
Zamiana indeksów |
Zamiana indeksów |
Zamiana podstawy |
1 |
y1 |
|
- |
|
|
2 |
y2 |
|
|
|
|
3 |
y3 |
|
|
|
|
4 |
y4 |
|
|
|
|
5 |
y5 |
|
|
|
|
Źródło: M. Sobczyk, Statystyka, W-wa 1991, s. 274
Indeksy jednopodstawowe i łańcuchowe pozwalają na ocenę zmian badanego zjawiska między dwoma wyróżnionymi okresami (momentami). Czasami zachodzi jednak konieczność oceny zmian danego zjawiska w całym okresie objętym obserwacją. Do tego celu wykorzystuje się średnią geometryczną.
Średnia geometryczna jest pierwiastkiem n - tego stopnia z iloczynu n zmiennych.
Średnie tempo zmian zjawisk ujętych w formie szeregów czasowych oblicza się najczęściej z indeksów łańcuchowych. Ponieważ jednak z n wielkości absolutnych można utworzyć n - 1 indeksów łańcuchowych, wzór na średnią geometryczną z indeksów łańcuchowych ma następującą postać:
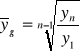
Wynika z powyższego, że wartość średniej geometrycznej jest pierwiastkiem stopnia n - 1 z ilorazu absolutnych poziomów badanego zjawiska z okresu (momentu) ostatniego i pierwszego.
Przykład 1
Na podstawie informacji dotyczących liczby zgonów ogółem w Polsce w latach 1970 - 1977 obliczyć średnie roczne tempo wzrostu tego zjawiska. (Sobczyk str. 277 w wydaniu z 1991)
Lata |
1970 |
1971 |
1972 |
1973 |
1974 |
1975 |
1976 |
1977 |
Zgony (w tys.) |
266,8 |
283,7 |
265,3 |
277,2 |
277,1 |
296,9 |
304,1 |
313 |
Po podstawieniu do wzoru otrzymujemy:
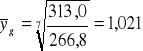
Otrzymany wynik oznacza, że liczba zgonów ogółem w Polsce w latach 1970 - 1977 wzrastała z roku na rok przeciętnie o 2,1%. (Przesunięcie przecinka o dwa miejsca i kasacja 1 z przodu)
Indeksy indywidualne i zespołowe (agregatowe)
wg formuły Laspeyresa i Paaschego.
Indeksy indywidualne znajdują zastosowanie w przypadku badania dynamiki zjawisk jednorodnych. Indeksem indywidualnym nazywamy wówczas stosunek poziomów tego samego pojedynczego zjawiska z dwóch różnych okresów (momentów).
W statystyce społeczno - ekonomicznej rozpatruje się zwykle trzy rodzaje indywidualnych wskaźników dynamiki: indeksy cen, indeksy ilości i indeksy wartości.
Indeks indywidualny cen wyraża relację poziomu cen określonego dobra w okresie badanym i w okresie podstawowym, co można zapisać następująco:
![]()
Gdzie: ip - indywidualny indeks cen; p1 - cena jednostki wyrobu (artykułu) w okresie badanym; p0 - cena jednostki wyrobu w okresie podstawowym.
Analogicznie oblicza się indywidualne indeksy ilości (iq) i wartości (iw) podstawiając do wzoru odpowiednio: q1 - ilość wyrobu wyprodukowanego w okresie badanym; q0 - ilość wyrobu wyprodukowanego w okresie podstawowym oraz w1 - wartość wyrobu w okresie badanym i w0 - wartość wyrobu w okresie podstawowym. Odpowiednie wzory wyglądają następująco:
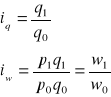
Indywidualne indeksy cen, ilości i wartości informują o zmianie (wzroście lub spadku) tych wartości w okresie badanym w porównaniu z okresem przyjętym za podstawę porównań.
Między indywidualnymi indeksami cen, ilości i wartości obliczonymi dla tego samego produktu zachodzi następujący związek:
![]()
Jest to tzw. równość indeksowa dla indeksów indywidualnych. Dzięki niej, nie dysponując informacjami wyjściowymi, można obliczyć wartość dowolnego indeksu znając wartości dwóch pozostałych indeksów.
W praktyce badań historycznych niejednokrotnie zachodzi konieczność obliczenia indeksów dotyczących nie indywidualnych jednostek, ale całego zespołu zjawisk - zazwyczaj niejednorodnych i bezpośrednio niesumowalnych. Stosuje się wówczas indeksy zespołowe (agregatowe).
Konstrukcja indeksów zespołowych opiera się na wykorzystaniu określonych współczynników przeliczeniowych, odgrywających rolę wag - zazwyczaj rolę tą pełnią ceny i ilości. W zależności od przedmiotu badań wyróżniamy indeksy zespołowe dla wielkości absolutnych i indeksy zespołowe dla wielkości stosunkowych.
Indeksy zespołowe dla wielkości absolutnych
Do grupy zespołowych indeksów dla wielkości absolutnych zalicza się agregatowy indeks wartości, ilości i cen.
Agregatowy indeks wartości określonego zespołu artykułów (wyrobów, produktów) jest ilorazem sum wartości badanych dóbr w okresie badanym i w okresie podstawowy:
![]()
Gdzie Iw - agregatowy indeks wartości badanego zespołu artykułów; Σq1p1 - suma wartości badanego zespołu w okresie badanym; Σq0p0 - suma wartości badanego zespołu w okresie podstawowym.
Agregatowy indeks wartości wyraża zmiany, jakie nastąpiły w badanym okresie w porównaniu z okresem podstawowym zarówno w ilościach zespołu artykułów jak i ich cenach. W celu obliczenia siły i kierunku zmian wyłącznie ilości lub wyłącznie cen buduje się odpowiednio agregatowe indeksy ilości (fizycznych rozmiarów, masy fizycznej) i agregatowe indeksy cen.
Konstrukcja agregatowych indeksów cen oparta jest na metodzie eliminacji, zwanej też standaryzacją wskaźników dynamiki. W przypadku indeksów agregatowych standaryzacja polega na ustaleniu stałego poziomu jednego z dwóch czynników: cen lub ilości. Dla uzyskania agregatowego indeksu ilości unieruchamiane są (ustalane na stałym poziomie) ceny. Natomiast dla uzyskania agregatowego indeksu cen unieruchamiane są ilości.
Wybór standaryzacji zależy od celu badania i posiadanych informacji statystycznych. Najczęściej wykorzystuje się formuły standaryzacyjne Laspeyresa i Paaschego.
Standaryzacja wg formuły Laspeyresa polega na unieruchomieniu ilości (obliczanie agregatowego indeksu cen) lub cen (obliczanie agregatowego indeksu ilości) na poziomie okresu podstawowego (bazowego).
Standaryzacja wg formuły Paaschego polega na unieruchomieniu ilości w indeksie cen lub cen w indeksie ilości na poziomie okresu badawczego (sprawozdawczego).
W zależności od przyjętej formuły można wyróżnić dwa rodzaje agregatowych indeksów cen i ilości.
Agregatowy indeks ilości wg formuły Laspeyresa ma postać:
![]()
Agregatowy indeks ilości wg formuły Paaschego ma postać:
![]()
Agregatowe indeksy ilości informują o tym, o ile - przeciętnie rzecz biorąc - wzrosła lub zmalała ilość określonego zbioru artykułów (wyrobów, produktów) w okresie badanym w porównaniu z okresem podstawowym (przy odpowiednim założeniu przyjętym w formule standaryzacyjnej)
Agregatowy indeks cen jest ilorazem sum wartości określonego zbioru artykułów w badanym czasie i sumy wartości tych samych artykułów w okresie podstawowym przy stałym „poziomie” ilości. Przy obliczaniu agregatowych indeksów cen rolę wag spełniają ilości.
Agregatowy indeks cen według formuły Laspeyresa:
![]()
Agregatowy indeks cen według formuły Paaschego:
![]()
Agregatowe indeksy cen odpowiadają na pytanie, jak zmieniły się - przeciętnie rzecz biorąc - ceny danego zbioru artykułów w okresie badanym w porównaniu z okresem podstawowym, przy unieruchomieniu ilości w obu okresach, zgodnie z przyjętą formułą standaryzacyjną.
Agregatowe indeksy cen i ilości obliczone wg formuł standaryzacyjnych Laspeyresa i Paaschego dla tego samego zespołu artykułów zwykle różnią się między sobą. Przyjmuje się, że jeżeli układ wyjściowy informacji na to pozwala, wskazane jest obliczenie indeksów wg obydwu formuł standaryzacyjnych.
Przykład 2
W pewnym przedsiębiorstwie produkującym trzy rodzaje wyrobów zebrano informacje dotyczące produkcji (w tys. sztuk) i cen jednostkowych (w tys. zł) tych wyrobów w dwóch latach: 1985 (okres podstawowy) i 1990 (okres badany).
Jak zmieniła się wartość produkowanych wyrobów w porównywanych okresach? Jaki wpływ na zmianę miała dynamika cen, a jaki dynamika ilości produkowanych wyrobów?
[Sobczyk str. 282 - 284 wyd. z 1991]
Wyrób |
Produkcja |
Ceny jednostkowe |
||
|
1985 (q0) |
1990 (q1) |
1985 (p0) |
1990 (p1) |
A B C |
0,8 1,0 1,5 |
1,2 1,4 1,3 |
24 18 30 |
30 20 35 |
Obliczenia pomocnicze
Wyrób |
q0 p0 |
q1 p1 |
q0p1 |
q1 p0 |
A B C |
19,2 18,0 45,0 |
36,0 28,0 45,5 |
24,0 20,0 52,5 |
28,8 25,2 39,0 |
Razem |
82,2 |
109,5 |
96,5 |
93,0 |
Podstawiając do wzoru na agregatowy indeks wartości otrzymujemy:
![]()
Oznacza to, że łączna wartość trzech wyrobów w 1990 r. jest o 33,21% wyższa od wartości w 1985 r. Wzrost wartości o 33,21% jest spowodowany zmianami cen i ilości produkowanych wyrobów.
Agregatowe indeksy ilości wg formuł Laspeyresa i Paaschego są równe:
![]()
Agregatowy indeks ilości typu Laspeyresa informuje o tym, ze produkcja trzech wyrobów łącznie (A,B,C) w 1990 r. w porównaniu z 1985 r. wzrosła o 13,14%, przy założeniu, że ceny w 1990 r. były takie same jak w 1985 r.
Agregatowy indeks ilości typu Paaschego informuje, ze produkcja łączna trzech wyrobów w 1990 r. wzrosła - w porównaniu z 1985 r. - o 13,47%, przy założeniu stałych cen w 1990 r.
Agregatowe indeksy cen wg formuł Laspeyresa i Paaschego są równe:
![]()
Agregatowy indeks cen typu Laspeyresa wskazuje, że cena badanych artykułów wzrosła w 1990 r. w porównaniu do 1985 r. o 17,4% - przy zachowaniu założenia, że w 1990 r. wyprodukowano taką samą ilość każdego wyrobu jak w 1985 r.
Agregatowy indeks cen typu Paaschego informuje, że ceny badanych produktów w 1990 r. wzrosły - średnio biorąc - w porównaniu z 1985 r. o 17,74% - przy założeniu, że w 1985 r. produkowano taką samą ilość wyrobów jak w 1990 r.
Indeksy zespołowe dla wielkości stosunkowych
Wielkości stosunkowe są wskaźnikami natężenia wyrażającymi stosunek dwóch zjawisk logicznie ze sobą powiązanych.
Przykładem wielkości stosunkowych mogą być takie kategorie jak:
wydajność pracy (iloraz produkcji i czasu pracy);
koszt jednostkowy (iloraz nakładów i wielkości produkcji);
średnia płaca (iloraz funduszu płac i zatrudnienia);
płodność (iloraz urodzeń żywych i ogólnej liczby kobiet w wieku rozrodczym);
umieralność (iloraz liczby zgonów i ogólnej liczby ludności).
Każdą wielkość stosunkową można rozpatrywać jako ogólną (zespołową) i cząstkową (jednostkową). Na przykład stosunek liczby urodzeń żywych w okresie t do liczby kobiet w wieku rozrodczym (15 - 49 lat) jest wielkością ogólną. Natomiast stosunek liczby urodzeń żywych w grupie kobiet w wieku 25 - 29 lat do ogólnej liczby kobiet w tym wieku jest wielkością stosunkową cząstkową.
Wielkości stosunkowe cząstkowe zapisujemy w postaci ułamka:
![]()
Wielkości stosunkowe ogólne (dotyczące całej badanej zbiorowości) zapisujemy w postaci ułamka:
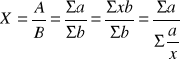
Narzędziem analizy dynamiki wielkości stosunkowych są indeksy wielkości stosunkowych. Oznaczając przez X1 ogólną wielkość stosunkową w badanym okresie, a przez X0 wielkość stosunkową w okresie podstawowym, możemy zapisać:
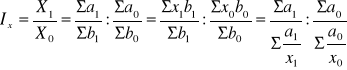
[Sposób: 1 2 3]
Indeks określony powyższym wzorem nosi nazwę agregatowego indeksu wszechstronnego, albo o zmiennej strukturze.
Jak wynika z powyższego można go obliczyć na trzy różne - ale równoważne - sposoby. Zastosowanie każdego z nich zależy od informacji, które posiadamy.
Pierwszy sposób obliczania wymaga znajomości poziomów czynnika a i b dla każdej cząstki zbiorowości i to w obydwu okresach (podstawowym i badanym).
Drugi sposób wymaga informacji o cząstkowych o wielkości stosunkowej x i czynnika b - jest to iloraz dwu średnich arytmetycznych ważonych (wagą jest czynnik b).
Jeżeli posiadamy informację o cząstkowych wielkościach stosunkowych oraz o czynniku a to możemy skorzystać ze sposobu trzeciego - iloraz dwu średnich harmonicznych ważonych (wagą jest czynnik a).
Drugi i trzeci sposób obliczania agregatowego indeksu wszechstronnego można również zapisać w innej postaci:
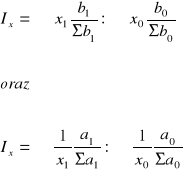
Wielkości ![]()
oraz ![]()
są wskaźnikami struktury informującymi o udziale cząstkowych wielkości b1 i b0 w globalnych wielkościach odpowiednio ![]()
oraz ![]()
. Analogicznie wielkości ![]()
oraz ![]()
są udziałami cząstkowych wielkości a1 i a0 w globalnych wielkościach ![]()
i ![]()
.
Pierwszy z powyższych wzorów określa zatem wszechstronny indeks struktury czynnika b. Natomiast wzór drugi określa wszechstronny indeks wielkości stosunkowych ważonych współczynnikami struktury czynnika a.
Wartość indeksu wszechstronnego jest wypadkową działania dwóch czynników, a mianowicie:
dynamiki cząstkowych wielkości stosunkowych;
zmian w strukturze czynnika a lub b.
Wpływ na dynamiki cząstkowych wielkości stosunkowych na poziom indeksu wszechstronnego określają indeksy zespołowe wielkości stosunkowych o stałej strukturze.
Przyjmując za niezmienne współczynniki struktury czynników a i b w okresie podstawowym (formuła Laspeyresa) otrzymujemy następujące wzory na indeksy o stałej strukturze:
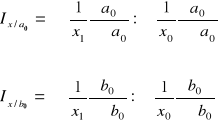
Przyjmując za niezmienne współczynniki struktury czynników a i b w okresie badanym (formuła Paaschego) otrzymujemy następujące wzory:
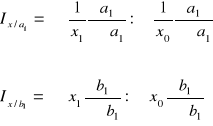
Wpływ zmian w strukturze czynników a i b na poziom indeksu wszechstronnego określają indeksy zespołowe zmian strukturalnych.
Indeks zmian strukturalnych typu Laspeyresa otrzymujemy przyjmując za stałe cząstkowe wielkości stosunkowe z okresu podstawowego. Agregatowe indeksy wpływu zmian w strukturze czynnika a i b typu Laspeyresa określają wzory:
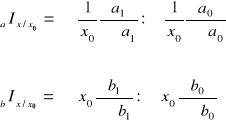
Indeks zmian strukturalnych typu Paaschego otrzymujemy przyjmując za stałe cząstkowe wielkości stosunkowe z okresu badanego. Agregatowe indeksy wpływu zmian w strukturze czynnika a i b typu Paaschego określają wzory:
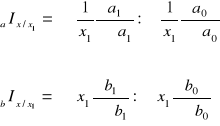
W konkretnym badaniu statystycznym dotyczącym analizy dynamiki wielkości stosunkowych o wyborze odpowiedniej postaci indeksów o stałej i zmiennej strukturze decydują względy merytoryczne.
Oblicza się indeksy o stałej i zmiennej strukturze tego z dwóch czynników a i b, który wywiera bezpośredni wpływ na dynamikę badanej wielkości stosunkowej. Np. bezpośredni wpływ na dynamikę urodzeń mają zmiany w strukturze kobiet w wieku rozrodczym (czynnik b). Dlatego też nie ma potrzeby obliczania indeksów o stałej i zmiennej strukturze czynnika a (liczba urodzeń).
Pomiędzy indeksem wszechstronnym a indeksami o stałej i zmiennej strukturze czynnika b, przy zachowaniu przemienności formuł Laspeyresa i Paaschego, zachodzą relacje:
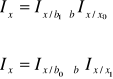
Analogiczny związek zachodzi między indeksem wszechstronnym a indeksem o stałej strukturze czynnika a i indeksem wpływu zmian w strukturze czynnika a:
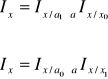
są tzw. równości indeksowe dla wielkości stosunkowych
Korzystając z tych relacji można pośrednio obliczyć jeden z trzech indeksów, jeżeli znane są dwa pozostałe.
Przykład 3
Na podstawie informacji zawartych w tabeli dokonać wszechstronnej analizy dynamiki płodności kobiet w Polsce w danym okresie [Sobczyk str. 288 - 291, wyd. z 1991]
Grupy
|
Cząstkowe współczynniki |
Liczebność kobiet |
||
|
1970 |
1977 |
1970 |
1977 |
|
x0 |
x1 |
b0 |
b1 |
15-19 20-24 25-29 30-34 35-39 40-44 45-49 |
30 165 126 71 36 11 1 |
34 169 133 70 31 9 1 |
1705,6 1458,6 939,4 1079,1 1129,6 1158,4 1071,3 |
1510,3 1714,9 1580,8 1086,3 999,5 1088,1 1154,2 |
Razem |
x |
x |
8542,0 |
9134,1 |
Informacje zawarte w tablicy pozwalają na obliczenie indeksu wszechstronnego:
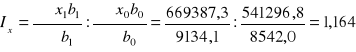
Oznacza to, ze ogólny poziom płodności w 1977 r. wzrósł w porównaniu z 1970 r. o 16,4%.
Na wzrost miały wpływ zmiany zarówno w cząstkowych współczynnikach płodności (dla poszczególnych grup wieku kobiet) jak i w strukturze kobiet według wieku.
Wpływ zmian w cząstkowych współczynnikach płodności na ogólny poziom płodności można zbadać za pomocą indeksu o stałej strukturze. Przyjmując za stałą (standardową) strukturę wieku kobiet w 1970 r. można obliczyć indeks o stałej strukturze czynnika b według formuły Laspeyresa. Natomiast przyjmując za standardową strukturę wieku kobiet w 1977 r. otrzymamy indeks o stałej strukturze czynnika b typu Paaschego.
Grupy |
x0 |
x1 |
|
|
|
|
|
|
15-19 20-24 25-29 30-34 35-39 40-44 45-49 |
30 165 126 71 36 11 1 |
34 169 133 70 31 9 1 |
0,200 0,171 0,110 0,126 0,132 0,136 0,125 |
0,165 0,188 0,173 0,119 0,109 0,119 0,127 |
6,80 28,90 14,63 8,82 4,09 1,22 0,13 |
6,00 28,22 13,86 8,95 4,75 1,50 0,13 |
5,61 31,77 23,01 8,82 3,38 107 0,13 |
4,95 31,02 21,80 8,45 3,92 1,31 0,13 |
Razem |
x |
x |
1,000 |
1,000 |
64,59 |
63,41 |
73,79 |
71,58 |
Indeks wpływu zmian w cząstkowych współczynnikach płodności wg formuły Laspeyresa (stała struktura wieku kobiet w 1970 r.) wynosi:
![]()
Po wyeliminowaniu różnych struktur wieku kobiet przez przyjęcie standardowej struktury z 1970 r. - ogólny współczynnik płodności z 1977 r. jest o 1,86% wyższy niż w 1970 r.
Indeks wpływu zmian w cząstkowych współczynnikach płodności wg formuły Paaschego (stała struktura wieku kobiet w 1977 r.) wynosi:
![]()
Przy założeniu stałej struktury wieku rozrodczego kobiet z 1977 r. ogólna płodność kobiet w 1977 r. wzrosłaby o 3,08% w porównaniu do 1970 r.
Wpływ zmian w strukturze wieku rozrodczego kobiet na dynamikę płodności można zbadać za pomocą indeksu wpływu zmian strukturalnych.
Przyjmując do obliczeń stałe cząstkowe współczynniki płodności kobiet z 1970 r. i podstawiając odpowiednie wielkości do wzoru na agregatowy indeks wpływu zmian w strukturze czynnika b typu Laspeyresa otrzymujemy:
![]()
Uzyskany wynik wskazuje, że gdyby cząstkowe współczynniki płodności w 1977 r. były takie same jak w 1970 r., to na skutek zmian w strukturze wieku rozrodczego kobiet nastąpiłby wzrost ogólnego współczynnika płodności o 12,88%.
Jeżeli przyjmiemy za niezmienne cząstkowe współczynniki płodności z 1977 r. i posłużymy się wzorem na agregatowy indeks wpływu zmian w strukturze czynnika b typu Paaschego otrzymujemy:
![]()
Oznacza to, że gdyby cząstkowe współczynniki płodności pozostały na poziomie z 1977 r., to ogólny poziom płodności w 1977 r. wzrósłby o 14,24% w porównaniu do 1970 r. Wzrost ten byłby spowodowany tylko i wyłącznie zmianami w strukturze wieku rozrodczego kobiet.
Na podstawie obliczonych indeksów można stwierdzić, że obserwowany w latach 1970 - 1977 wzrost płodności kobiet (o 16,4%) jest wynikiem zarówno efektywnego wzrostu płodności kobiet w poszczególnych grupach wieku (z 1,86% do 3,08%) jak i korzystnych zmian w strukturze wieku kobiet (z 12,88% do 14,24%).
Wyszukiwarka
Podobne podstrony:
szeregi czasowe sciagawka, Ekonometria szeregów czasowych, Welfe, eszcz
analiza ekonomiczna browary (13 stron) 6BZ3TQZDMJLKTO3CGTQIDQL5Q3Q4FRKYLPFNRRY
raport marketingowy płatna tv (13 stron) qtz6zfge7wct7mqr4j3ydtvxpzpu6n5kpfltaiq QTZ6ZFGE7WCT7MQR4
11 Analiza Szeregów Czasowych z rozwiązaniami
Ekonometria szeregow czasowych Nieznany
Charakterystyka nowoczesnej koncepcji logistyki (13 stron), Logistyka
Finanse-przedsiebiorstw-(13-stron), Finanse
Zrównoważony rozwój w turystyce (13 stron) GZJPEUVJQE22OSEWS6I7UWWGLZFRXP6VBO6GT4Q
Analiza szeregów czasowych wzory
Papiery wartościowe notowane na?TO (13 stron) VGCFUFY2QO2FVBSUSMFCZL2SIWBP7ZORPRCXQIQ
Kalkulacja (13 stron) UXAUYFXTY67G4Z2BE7J2ACLOEJFYY25GLE3V3OA
Segmentacja rynku (13 stron) 6VWFKRDC6DNEY3S7VY2EDOH3SV5SEFXK3GOP4TI
Znaczenie systemu ocen pracowników (13 stron) KZ74NGQMUEN4PZPRTE677ONKJ4QXW3WHQOV5ANA
więcej podobnych podstron