1. WSTĘP

Istotną rolę podczas przepływów zarówno cieczy , jak i gazów przez przewody lub podczas ruchu względem innego ośrodka odgrywa opór lepki , zwany tarciem wewnętrznym. Właściwość ta mierzona jest ilościowo współczynnikiem lepkości. W warstwie cieczy o grubości h , ograniczoną płaszczyznami A i B , sile zewnętrznej przeciwdziała siła lepkości i zgodnie z I zasadą dynamiki mamy ruch jednostajny płyty B . W warstwie cieczy ustala się stały gradient prędkości . Dla większości cieczy spełniona jest zależność wprowadzona przez Newtona :

Ciecze stosujące się do powyższego prawa nazywamy cieczami newtonowskimi. Współczynnik lepkości cieczy newtonowskich maleje wraz ze wzrostem temperatury zgodnie z zależnością :

gdzie :

W - energia aktywacji,

k - stała Boltzmanna .

Wielkość A słabo zależy od temperatury i w naszym przypadku można ją uznać za stałą .

Współczynnik lepkości mierzy się tzw. wiskozymetrami . Najczęściej wykorzystuje się wiskozymetry wykorzystujące zjawiska :

1. ruchu jednostajnego ciał stałych w płynie lepkim , np.wiskozymetr Stokesa , Hopplera .

2. przepływu płynu przez rurki kapilarne , np. wiskozymetr Ostwalda .

WISKOZYMETR HOPPLERA .

Cechą charakterystyczną tego przyrządu jest nachylenie rury pomiarowej pod kątem ok. 10^o. Kulka szklana lub metalowa ( zależnie od lepkości cieczy ) posiada średnicę bliską średnicy wewnętrznej rury , dzięki czemu wydłuża się czas opadania kulki . Siła oporu ze strony cieczy jest proporcjonalna do prędkości toczenia się kulki :

gdzie:

k - współczynnik proporcjonalności stały dla danego przyrządu .

Rozkładając siły ciężkości i wyporu na składowe styczne i normalne otrzymamy warunek równowagi sił :

Po wstawieniu wyrażeń na masę kulki i siłę wyporu otrzymamy :

Prędkość ruchu jednostajnego:

.

gdzie l - odległość między skrajnymi rysami rury pomiarowej

więc ostatecznie otrzymamy :

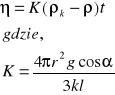
jest stałą aparaturową .

Rura pomiarowa , wypełniona badaną cieczą ( w naszym przypadku olejem parafinowym ), umieszczona jest w kąpieli wodnej . Do pomiaru temperatury służy termometr rtęciowy . Do prawidłowego ustawienia przyrządu służy libella i śruby regulacyjne w podstawie . Na rurze pomiarowej wytrawiono trzy rysy . Zaleca się , by pomiar czasu opadania przeprowadzać dla skrajnych rys.

2. PRZEBIEG ĆWICZENIA

1.Sprawdzamy prawidłowość ustawienia wiskozymetru przy pomocy poziomicy.

2.Zmieniamy temperaturę cieczy przy pomocy ultratermostatu z termometrem kontaktowym w granicach od temperatury pokojowej do 50°C, mierzymy czas opadania kulki między skrajnymi poziomami obserwacyjnymi.

3.Dla każdej temperatury mierzymy czas przy pomocy dwóch stoperów.

3. POMIARY I OBLICZENIA

Wyniki pomiarów zestawiono w tabeli.

Lp.	Temperatura T [°C]	Czas opadania kulki t [s] Dla stopera pierwszego	Czas opadania kulki t [s] Dla stopera drugiego	Średni zas opadania kulki t [s]
1	22	208,60	209,20	208,9
2	25	174,35	173,80	174,075
3	27	149,40	149,10	149,25
4	29,5	133,60	134,20	133,9
5	34	103,28	102,80	103,04
6	36,5	85,16	86,74	85,95
7	39,5	75,46	75,10	75,28
8	42	64,48	63,90	64,19
9	45,5	54,25	54,90	54,575
10	49,5	45,60	46,15	45,875

Na podstawie tabeli w skrypcie wykonujemy wykres temperaturowej zależności gęstości oleju parafinowego.

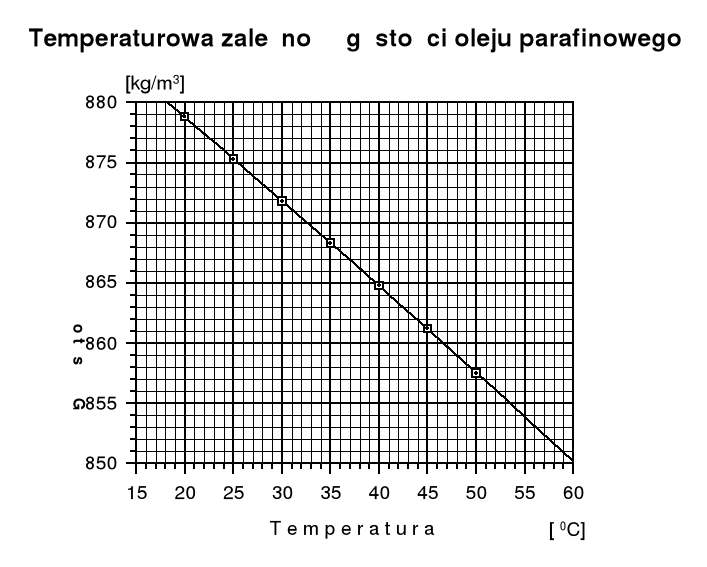
Na podstawie wykresu odczytujemy gęstość oleju w temperaturach pomiarowych. Dla każdej temperatury obliczamy współczynnik lepkości oleju parafinowego stosując wzór empiryczny:

η=K(ρ_k-ρ)t

gdzie: K=1.2018∗10^-6 m²/s²

ρk=8150 kg/m³

ρ - gęstość oleju parafinowego odczytujemy z tabeli:

Temperatura [°C]	Gęstość oleju [kg/m^3]	Obliczony Współczynnik Lepkości [ kg / m * s]
22	877,5	1,823
25	875,5	1,521
27	874	1,305
29,5	872,1	1,171
34	869	0,902
36,5	867,5	0,752
39,5	865	0,675
42	863,2	0,562
45,5	860,7	0,478
49,5	857,8	0,402

Wykonujemy wykres zależności logarytmu współczynnika lepkości w funkcji odwrotności temperatury:

ln η= f ( 1 / T)

l.p	ln η [N s/ m^2]	1/T *10^-4 [1/K]
1	0,600	3,13
2	0,420	3,101
3	0,266	3,082
4	0,158	3,058
5	-0,103	3,016
6	-0,285	2,994
7	-0,362	2,967
8	-0,576	2,945
9	-0,738	2,915
10	-0,911	2,881

Metodą regresji liniowej wyliczamy (przy pomocy programu komputerowego) współczynniki dla podanych wyżej wartości.

Wyniki przedstawiają się następująco:

Współczynnik a =		6,11*10^3
Współczynnik b =		-18,531
Błąd Sa =	0,12*10^3
Błąd Sb =	0,041
Wsp. Korelacji =		0.99853

Obliczamy współczynniki A i W/k.

ln η = e ^-18,6 ∗ e^{1/ T ⋅ 6110}

więc: A = e ^-18,6 =8,36*10^-9

W/k = 6110

5. DYSKUSJA BŁĘDÓW

Dla potrzeb dyskusji błędów przyjmiemy , że błąd pomiaru czasu wynosił 1.5 sekundy. Podyktowane jest to tym , że trudno było jednoznacznie określić moment w którym krawędź kulki zrównywała się z cechą na wiskozymetrze (błąd paralaksy). Należy także uwzględnić czas reakcji przy załączaniu i zatrzymywaniu stopera.

 t = 1.5 [s]

Obliczamy błąd dla gęstości oleju parafinowego . Z wykresu wynika, że temperaturowa zależność gęstości oleju parafinowego jest zależnością liniową. Zmiana temperatury o 1°C powoduje zmniejszenie gęstości o 0.78 kg/m³.

Dokładność pomiaru temperatury : ΔT = 0.5°C.

Więc gęstości oleju parafinowego są obarczona błędem : Δρ = 0.39 kg/m³.

Do obliczenia błędu używamy metody różniczki zupełnej .

η = K t (ρ_k - ρ)

Różniczkując otrzymujemy:

Ostatecznie: Δη = K (ρ_k - ρ) ∗ Δt + K∗t ∗Δρ

Obliczamy błędy lepkości dla poszczególnych temperatur pomiarowych.

Dla 295 K:

Δη₁ = 1.2018∗10^-6∗(8150-877.5)∗1.5 +1.2018∗10^-6∗295 ∗0.39=0.0132 [N s/m²]

Dla 298 K: Δη₂ = 0,0132 [N s/m²]

Dla 300 K: Δη₃ = 0,0132 [N s/m²]

Dla 302,5 K: Δη₄ = 0,0132 [N s/m²]

Dla 307 K: Δη₅ = 0,0132 [N s/m²]

Dla 309,5 K: Δη₆ = 0,0132 [N s/m²]

Dla 312,5 K: Δη₇ = 0,0132 [N s/m²]

Dla 315 K: Δη₈ = 0,0132 [N s/m²]

Dla 318,5 K: Δη₉ = 0,0132 [N s/m²]

Dla 322,5 K: Δη₁₀ = 0,0130 [N s/m²]

6. WYNIK ĆWICZENIA

Wyznaczyliśmy następujące lepkości oleju parafinowego:

Temperatura [^0C]	Współczynnik lepkości  [N s/m^2]
22	1,823±0,014
25	1,521±0,014
27	1,305±0,014
29,5	1,171±0,014
34	0,902±0,014
36,5	0,752±0,014
39,5	0,675±0,014
42	0,562±0,014
45,5	0,478±0,014
49,5	0,402±0,013

Zależność lepkości od temperatury przedstawia równanie.

η = 8,36*10^-9 * e^{1 / T ∗6110} [N*s/m²]

7. WNIOSKI

Temperaturowa zależność współczynnika lepkości oleju parafinowego jest zależnością eksponencjalną - lepkość maleje wraz ze wzrostem temperatury. Zaistniałe błędy są spowodowane niedokładnościami podczas odczytu czasu spadania kulki. Wpływ na to miało pewne opóźnienie wyłączenia i włączenia stoperów, a także niedokładne wychwycenie momentu przekroczenia przez kulkę rys pomiarowych - mieliśmy tutaj do czynienia z błędem paralaksy. Wartość temperatury

wskazanej przez termometr podlegała pewnym wahaniom spowodowanym bezwładnością termostatu w nagrzewnicy.

---