1. CEL ĆWICZENIA :
Celem ćwiczenia jest wyznaczenie zdolności emisyjnej powierzchni grzejnika metodą porównawczą.
2. WPROWADZENIE :
Wymiana ciepła przez promieniowania, w ujęciu fenomenologicznym, opiera się na przekształceniu energii wewnętrznej w energię fal elektromagnetycznych promieniowania termicznego. Fale te przedostają się przez ośrodek przezroczysty do drugiego ciała, gdzie ponownie zamienia ją się w energię wewnętrzną.
Powyższe zagadnienie rozpatrywane w ujęciu statystycznym sprowadza promieniowanie do przenoszenia energii za pomocą fotonów, które opuszczają jedne atomy i zostają pochłonięte przez inne.
Promieniowanie każdego ciała składa się z emisji własnej i odbitej.
Dla każdego ciała możemy zapisać:
![]()
gdzie :
e - gęstość strumienia emisji
E - strumień emisji
A - powierzchnia emitująca
Zdolność emisyjną ε zapisujemy:
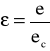
gdzie :
e- emisyjność ciała doskonale czarnego definiowana na podstawie prawa Stefana-Boltzmanna w następujący sposób:
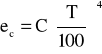
gdzie :
C- stała promieniowania
T- temperatura
3. PRZEBIEG ĆWICZENIA:
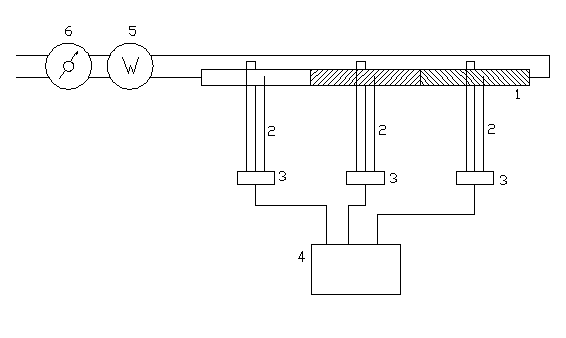
Podczas ćwiczenia dokonano pomiarów wskazań z 9 termopar (po trzy na jeden odcinek rury), na stanowisku jak na rysunku 1. Wyniki pomiarów 1 (przy mocy 22,5W) i 2 (przy mocy 36W) umieszczono w tabelach 1 i 2.
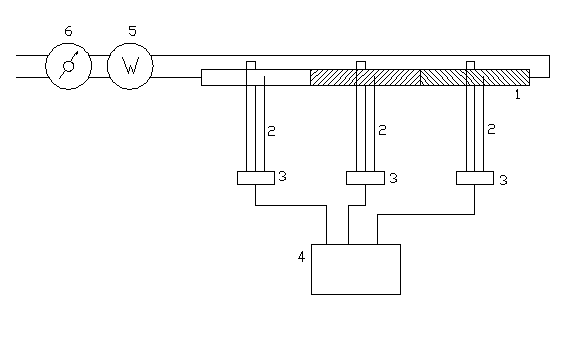
Rysunek 1. Schemat stanowiska pomiarowego (1-rura grzejna, 2-termopary, 3-zimne końce termopar,4-rejstrator, 5-watomierz, 6-autotransformator).
Tabela 1:
|
ΔE, mV |
||||||||
Δt,min |
1 |
2 |
3 |
5 |
6 |
7 |
9 |
10 |
11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0,45 |
0,45 |
0,45 |
0,75 |
0,75 |
0,75 |
0,4 |
0,4 |
0,4 |
4 |
0,71 |
0,71 |
0,83 |
1,05 |
1,05 |
1,05 |
0,72 |
0,72 |
0,71 |
6 |
0,95 |
0,95 |
1,05 |
1,32 |
1,32 |
1,32 |
0,85 |
0,85 |
0,85 |
7 |
1,01 |
0,97 |
1,1 |
1,41 |
1,41 |
1,39 |
0,9 |
0,9 |
0,87 |
8 |
1,05 |
1,03 |
1,14 |
1,45 |
1,45 |
1,41 |
0,95 |
0,94 |
0,89 |
9 |
1,07 |
1,04 |
1,15 |
1,49 |
1,49 |
1,49 |
0,95 |
0,95 |
0,91 |
10 |
1,09 |
1,06 |
1,19 |
1,52 |
1,52 |
1,51 |
0,95 |
0,95 |
0,91 |
Tabela 2:
|
ΔE, mV |
||||||||
Δt,min |
1 |
2 |
3 |
5 |
6 |
7 |
9 |
10 |
11 |
2 |
1,25 |
1,25 |
1,39 |
1,83 |
1,83 |
1,80 |
1,20 |
1,20 |
1,13 |
4 |
1,55 |
1,48 |
1,66 |
2,18 |
2,16 |
2,06 |
1,38 |
1,38 |
1,32 |
5 |
1,64 |
1,53 |
1,74 |
2,29 |
2,29 |
2,20 |
1,44 |
1,44 |
1,36 |
6 |
1,65 |
1,60 |
1,80 |
2,32 |
2,32 |
2,28 |
1,46 |
1,46 |
1,36 |
7 |
1,69 |
1,60 |
1,81 |
2,37 |
2,37 |
2,34 |
1,46 |
1,46 |
1,38 |
8 |
1,71 |
1,66 |
1,84 |
2,33 |
2,29 |
2,29 |
1,46 |
1,47 |
1,39 |
9 |
1,70 |
1,64 |
1,85 |
2,38 |
2,38 |
2,31 |
1,49 |
1,49 |
1,39 |
10 |
1,74 |
1,63 |
1,88 |
2,39 |
2,39 |
2,29 |
1,48 |
1,48 |
1,36 |
![]()
Odczytano również temperaturę otoczenia
POMIAR 1:
Następnie wyznaczamy różnic temperatury średniej termopar i otoczenia
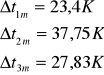
Następnie temperaturę bezwzględną termopar i temperaturę ścian pomieszczenia:
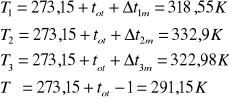
Strumień ciepła dostarczony do każdego odcinka rury można zapisać:
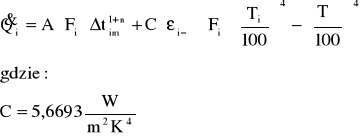
F- pole powierzchni zewnętrznej odcinka rury
stały współczynnik proporcjonalności
n- wykładnik zależny od liczb kryterialnych (n=25)
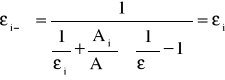
gdyż:
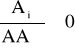
stąd:
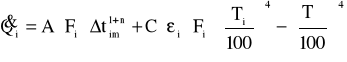
Ponieważ każdy odcinek rury został zaopatrzony w taką samą ilość ciepła otrzymujemy układ równań:
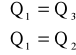
Po podstawieniu wartości otrzymujemy:
![]()
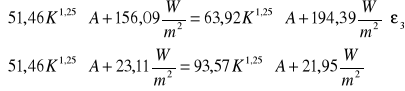
Z drugiego równania wyznaczono stałą proporcjonalności A=0,9 W/(m K ). Równanie pierwsze natomiast przyjmuje postać:
POMIAR 2:
Następnie wyznaczamy różnic temperatury średniej termopar i otoczenia
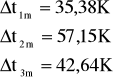
Następnie temperaturę bezwzględną termopar i temperaturę ścian pomieszczenia:
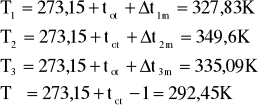
Strumień ciepła dostarczony do każdego odcinka rury można zapisać:
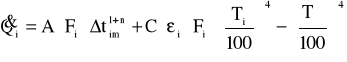
Ponieważ każdy odcinek rury został zaopatrzony w taką samą ilość ciepła otrzymujemy układ równań:
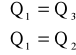
Po podstawieniu wartości otrzymujemy:
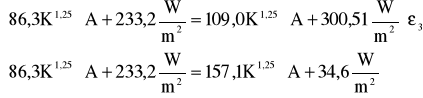
Z drugiego równania wyznaczono stałą proporcjonalności A=2,81 W/(m K ). Równanie pierwsze natomiast przyjmuje postać:
![]()
Znając stałą A dla obydwu pomiarów wyznaczono współczynnik wnikania ciepła dla konwekcji swobodnej:
![]()
Wyniki umieszczono w tabeli 3.
|
Współ. wnikania ciepła, W/(m. K) |
|
i |
POMIAR 1 |
POMIAR 2 |
1 |
6,05 |
6,85 |
2 |
6,87 |
7,72 |
3 |
6,31 |
7,18 |
![]()
4. WNIOSKI:
Otrzymana zdolność emisyjna jest porównywalna ze zdolnością emisyjną miedzi zawartej w tablicach.
Zdolność emisyjna przyjmuje zawsze wartości z przedziału od 0 do 1, co oznacza, że żadne ciało rzeczywiste nie posiada gęstości strumienia emisji równej gęstości strumienia emisji ciała doskonale czarnego.
Wartości otrzymane w pomiarach 1 i 2 są w granicach błędu pomiarowego, co dowodzi iż emisyjność jest wielkością niezależną od strumienia dostarczonego ciepła.
![]()
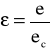
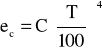
![]()
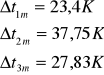
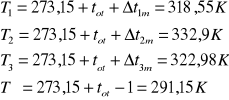
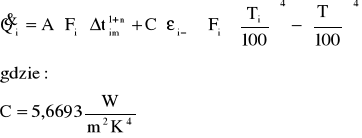
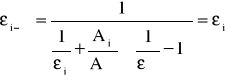
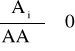
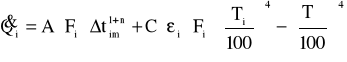
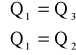
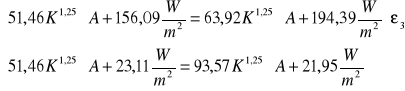
![]()
![]()
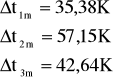
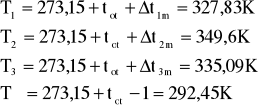
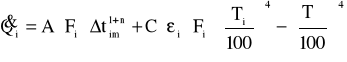
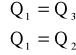
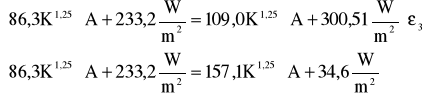
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Wyznaczanie współczynnika napięcia powierzchniowego cieczy metodą kapilary pionowej, Fizyka
Wyznaczanie współczynnika napięcia powierzchniowego cieczy metodą kapilary pionowej(1)
Wyznaczanie napięcia powierzchniowego cieczy metodą stalagmometryczną, Technologia chemiczna, Chemia
33. WYZNACZANIE MAŁYCH OPORÓW METODĄ PORÓWNYWANIA, Pracownia fizyczna, Moje raporty
Porównanie skuteczności ujawniania śladów linii papilarnych na mokrych powierzchniach papierowych me
111-4, materiały studia, 111. WYZNACZANIE SZEROKOŚCI PRZERWY ENERGETYCZNEJ W PÓŁPRZEWODNIKU METODĄ T
Wycena nieruchomości gruntowej metodą porównywania parami
Wyznaczanie prędkości?l akustycznych w ciałach stałych metodą Kundta
7.4, 7.4 , Pomiar napięcia powierzchniowego cieczy metodą stalagmometryczną
Dobór powierzchni grzejników konwekcyjnych
Wyznaczanie współczynnika lepkości cieczy biologicznych metodą Stokesa
C6B Wyznaczanie współczynnika napięcia powierzchniowego
19 Warstwy powierzchniowe otrzymywane metodami chemicznymi i elektrochemicznymi
21 Wyznaczanie pracy wyjścia elektronów z metalu metodą prostej Richardsona
laborka37, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdani
sprawko 3, Ocena Krajobrazu metodą porównań bezpośrednich
119, 119jkn, TEMAT: Pomiar napięcia powierzchniowego cieczy metodą
Wyznaczanie grubości cienkiej folii aluminiowej metodą pochł
więcej podobnych podstron