Politechnika Krakowska Fizyka Techniczna	Górski Paweł	Rok akad.: 1999/2000		Data: 2.11.1999
Grupa 1 Zespół 7		Nr ćwicz.: 31	Ocena:		Podpis:

Temat:

Badanie rezonansu w obwodzie RLC

Wartością chwilową nazywamy wartość, jaką sygnał przyjmuje w danej chwili.

Wartością szczytową (maksymalną) sygnału nazywamy największą wartość chwilową, jaką sygnał osiąga w rozpatrywanym przedziale czasu.

Wartością średnią półokresową sygnału okresowego o okresie T nazywamy średnią arytmetyczną tego sygnału obliczoną dla połowy okresu :

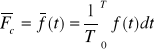
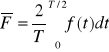
Wartością średnią całookresową sygnału okresowego w okresie T nazywamy średnią arytmetyczną tego sygnału obliczoną dla jednego okresu T :

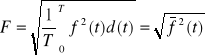
Wartością skuteczną sygnału okresowego o okresie T nazywamy pierwiastek kwadratowy z wartości średniej kwadratu sygnału obliczonej dla jednego okresu T

Wartości skutecznej prądu można nadać następującą interpretację fizyczną : wartością skuteczną prądu okresowego nazywamy taką wartość prądu stałego, który przepływając przez niezmienną rezystancję R w czasie okresu T, spowoduje wydzielenie na tej rezystancji takiej samej ilości ciepła , co prąd okresowo zmienny w tym czasie.

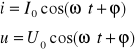
Prądem zmiennym nazywa się prąd którego natężenie i napięcie zmienia się sinusoidalnie :

i - natężenie chwilowe, u- napięcie chwilowe, I₀ - natężenie maksymalne, U₀ - napięcie szczytowe

jest częstością kołową lub pulsacyjną, ν=T^-1 - częstością lub częstotliwością, T- okresem, ωt - argumentem, a ϕ - fazą początkową.

Przepływem prądu zmiennego, podobnie jak stałego, rządzą prawa Kirchoffa, lecz inaczej tu zachowuję się cewki i kondensatory. Prąd przemienny przepływa przez kondensator, przy czym przewodzenie prądu polega na ładowaniu kondensatora raz w jednym, a za pół okresu w przeciwnym kierunku.

Napięcie U_c na okładkach wyraża się wzorem

Gdzie: Q- ładunek na okładkach kondensatora, a C - jego pojemność.

Dla cewki istotną rolę odgrywa indukcja własna, z która związana jest siła elektromotoryczna

gdzie L - współczynnik indukcji własnej.

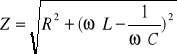
Jeżeli obwód zawiera równocześnie opornik „omowy” o oporze R, kondensator o pojemności C oraz cewkę o indukcji własnej L, to rolę oporu spełnia impedancja Z, wyrażona wzorem :

Prawo Ohma wiąże maksymalne wartości napięcia i prądu :

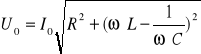
Układ szeregowy RLC

W tym obwodzie II prawo Kirchoffa przyjmuje postać :

przyjmując, że

i po zróżniczkowaniu otrzymujemy

i jest to różniczkowe równanie drgań wymuszonych w szeregowym obwodzie RLC.

Równanie to posiada rozwiązanie postaci

Prąd zmienny I=I₀ sinω t płynąc przez opór omowy R wywołuje spadek napięcia

U = I₀Rsinω t

Nie ma zatem przesunięcia fazowego między prądem i napięciem a zawada omowa (rezystancja) jest równa R. Natomiast I=I₀ sinω t płynąc przez cewkę o indukcyjności L (dla której R=0) wywołuje spadek napięcia :

Widzimy więc, że napięcie wyprzedza prąd o π/2 lub prąd opóźnia się za napięciem o π/2.

Reaktancja indukcyjna :

Podobnie prąd zmienny I=I₀sinω t płynąc przez kondensator, o pojemności C wywołuje spadek napięcia :

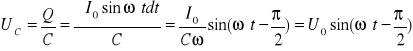
W tym przypadku napięcie jest opóźnione za prądem o -π/2, prąd wyprzedza napięcie o π/2.

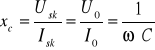
Reaktancja pojemnościowa :

Rezonans napięć występuje w obwodzie szeregowym RLC, wówczas gdy U_L=U_C (X_L=X_C); Z=R, a prąd uzyskuje maksymalną wartość

Przy rezonansie φ=0, a moc czynna jest równa mocy całkowitej.

Pomiar 1

Badanie rezonansu w szeregowym obwodzie RLC.

Parametry elementów obwodu:

• opór R₁ = 50 Ω, ale miliamperomierz też posiada opór R_A = 185 Ω, więc

R₁ = 50 + 185 Ω = 235 Ω

oraz R₂ równy rezystancji wewnętrznej miliamperomierza

R₂ = 185 Ω

• pojemność C = 1 μF

• indukcyjność L = 70 mH, ale i tu miernik posiada własną L_A = 30 mH, więc

L = 70 + 30 mH = 100 mH

Dla ustalonych wartości parametrów obwodu obliczam częstotliwość rezonansową

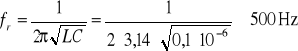
Pomiary wykonywaliśmy dla częstotliwości f_r ± 300 Hz, przy stałym napięciu U.

Lp	Usk [V]	f [Hz]	R1		R2
			Isk [mA]	Z [Ω]	Isk [mA]	Z [Ω]
1	4	200	5,35	747,7	5,5	727,3
2	4	250	6,85	583,9	7,21	554,8
3	4	300	8,55	467,8	9,05	442,0
4	4	350	10,25	390,2	11	363,6
5	4	400	11,39	351,2	12,6	317,5
6	4	450	12,4	322,6	13,5	296,3
7	4	475	12,6	317,5	13,7	292,0
8	4	490	12,7	315,0	13,85	288,8
9	4	495	12,7	315,0	14,1	283,7
10	4	496	12,7	315,0	14,1	283,7
11	4	497	12,7	315,0	14,1	283,7
12	4	498	12,7	315,0	14,1	283,7
13	4	499	12,7	315,0	14,1	283,7
14	4	500	12,7	315,0	14,1	283,7
15	4	501	12,7	315,0	14,1	283,7
16	4	502	12,7	315,0	14,1	283,7
17	4	503	12,7	315,0	14,1	283,7
18	4	504	12,69	315,2	14,1	283,7
19	4	505	12,68	315,5	14,1	283,7
20	4	510	12,65	316,2	14,1	283,7
21	4	525	12,6	317,5	14,09	283,9
22	4	550	12,55	318,7	13,95	286,7
23	4	600	12,15	329,2	13,2	303,0
24	4	650	11,65	343,3	12,55	318,7
25	4	700	11,09	360,7	11,89	336,4
26	4	750	10,25	390,2	10,95	365,3
27	4	800	9,68	413,2	10,29	388,7
28	4	850	9	444,4	9,62	415,8
29	4	900	8,51	470,0	9,05	442,0

Schemat układu pomiarowego.

wykres nr 1. Przedstawiający zalezność prądu od częstotliwości w obwodzie szeregowym dla 2 różnych rezystancji

Pomiar 2

Badanie rezonansu w obwodzie równoległym RLC.

Schemat układu pomiarowego.

Parametry elementów obwodu:

• opór R = 3 kΩ

• pojemność C = 1 μF

• indukcyjność L = 70 mH

Dla ustalonych wartości parametrów obwodu obliczam częstotliwość rezonansową

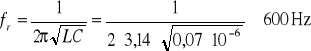
Pomiary wykonywaliśmy dla częstotliwości f_r ± 300 Hz, przy stałym napięciu U.

Lp	Usk [V]	f [Hz]	Isk [mA]	Z [Ω]
1	3	300	8,1	370,4
2	3	350	7,25	413,8
3	3	400	6,3	476,2
4	3	450	5,35	560,7
5	3	500	4,4	681,8
6	3	550	3,6	833,3
7	3	600	3	1000,0
8	3	610	3	1000,0
9	3	620	3	1000,0
10	3	630	3	1000,0
11	3	640	3,1	967,7
12	3	650	3,2	937,5
13	3	700	3,9	769,2
14	3	750	5	600,0
15	3	800	6,2	483,9
16	3	850	7,45	402,7

wykres nr 2. Przedstawiający zależność prądu od częstotliwości w obwodzie równoległym

1

2

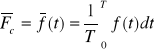
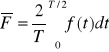
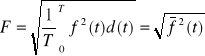
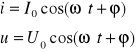
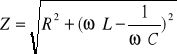
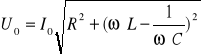
U

L

R

C

U_R

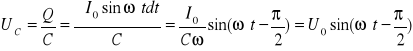
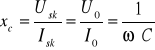
U_C

U_L

I

U

R

C

L

mA

V

Generator

U_R

U_C

U_L

I

U

R

C

L

mA

V

Generator

---