Zestaw C

1) Zbadano czas rozmów 50 połączeń:

Czas trwania rozmów	Liczba połączeń	x'	x' n	(x'-xśr)^2⋅n	cum ni
0-4 4-8 8-12 12-16 16-20	10 16 12 9 3	2 6 10 14 18	2⋅10=20 6⋅16=96 10⋅12=120 14⋅9=126 18⋅3=54	(2-8,32)^2⋅10=399,42 (6-8,32)^2⋅16=86,12 (10-8,32)^2⋅12=33,87 (14-8,32)^2⋅9=290,36 (18-8,32)^2⋅3=281,11	10 26 38 47 50
Suma	50	X	416	1090,88	X

Zbiorowość: Połączenia

Jednostka: 1 połączenie

Cecha statystyczna zmienna: Czas trwania rozmów (chyba w minutach) - cecha rzeczowa, mierzalna, ciągła

Kompleksowa analiza struktury:

Przeprowadzamy na miarach klasycznych, gdyż wszystkie przedziały są zamknięte i mają równą rozpiętość

Wyniki:

• Średnia: 8,32 minut

• Odchylenie: 4,67 minut

• Współczynnik zmienności: 56,14 %

• Typowy obszar zmienności: 8,32 - 4,67 < Xtyp < 8,32 + 4,67

• Zamiast liczyć alfa3 można zastąpić go As

• Modalna: 6,40 minut

• Mediana: 7,75 minut

• Klasyczno-pozycyjny wsp. asymetrii: 0,41

2) Dane są następujące indeksy:

Lata	Indeksy (1992=100)	<= To są indeksy stałe (jednopodstawowe) o podstawie w roku 1992 (1992=100%)
1990 1991 1992 1993 1994 1996 1996 1997 1998	108,6 113,0 100,0 107,2 130,7 173,5 185,3 195,2 214,0

Wyznacz wartość eksportu dla wszystkich lat wiedząc, że w 1990 roku wynosił on 14,32 mld PLN - Najprościej układać sobie proporcje, rok po roku, ale zacząć od 1990 i 1992

(1990) 108,6 = 14,32 mld

(1992) 100,0 = X

Mając wartość w 1992 roku będzie się liczyło łatwiej bo się będzie porównywało ze 100,0

Wyznacz średnie tempo zmian oraz postaw prognozę na 1999 rok

Liczymy średniookresowe tempo zmian (i z daszkiem) najlepiej podstawiając do wzoru ostatni i pierwszy indeks stały:

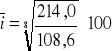
= 108,85

dlatego 8 bo n−1 czyli 9 lat − 1

Odp. W latach 1990-1998 co roku wartość eksportu rosła średnio o 8,85%

Prognozę zapisujemy tak:

y(1999) = 14,32 ⋅ (1,0885)⁹ = 30,72

dlatego do 9 potęgi bo takich przyrostów od 1990 do 1999 jest właśnie 9

3)

Dane są następujące informacje na temat produkcji tkanin (X) oraz czasu ich wyrobu (Y):

Średni X = 600

Średni Y = 160

Vx = 30% => Trzeba wyliczyć odchylenie X = 180

Vy = 25% => Trzeba wyliczyć odchylenie Y = 40

r_xy = 0,80

Wyznacz obie funkcje regresji => Ze wzorów uproszczonych - wykorzystujemy odchylenia, r_xy oraz średnie

Oszacuj czas wyrobu dla 1000 sztuk tkanin - podstawiamy do funkcji regresji x=1000 i PAMIĘTAĆ
O +- Sy

W jakim stopniu produkcja determinuje czas wyrobu? => Trzeba wyznaczyć współczynnik determinacji (d)

d = r_xy² ⋅ 100 = 64 %

4)

Funkcja trendu y^ = 2,2 + 0,4 t (t=...,-3,-1,1,3,...) opisuje spożycie bananów w kwartałach - NIE SPISAŁEM JAKIE LATA :(

Średni błąd szacunku czyli Sy = 0,03 kg

Surowe wskaźniki sezonowości:

I 1,0 II 0,9 III 0,6 IV 1,8

Postaw prognozę na II kwartał 2006 roku

Najpierw trzeba oczyścić !!! surowe wskaźniki (bo ich suma wynosi 4,3 czyli jest za duża)

4,3 dzielimy przez 4 to daje wsp. korygujący k=1,075

Wszystkie wsk. surowe dzielimy przez k=1,075 i otrzymujemy wskaźniki oczyszczone:

I 0,93 II 0,84 III 0,56 IV 1,67

Potem podstawiamy odpowiedni okres (t) do funkcji trendu i wynik mnożymy przez oczyszczony !!! wskaźnik dla II kwartału (tj. przez 0,84) - PAMIĘTAĆ JESZCZE O +- Sy czyli 0,03

5) Odchylenie ćwiartkowe jest miarą:

1. asymetrii

2. koncentracji

3. zróżnicowania

6) Wahania sezonowe to:

1. długookresowa dążność do wzrostu lub spadku

2. regularne zmiany okresowe o cyklu rocznym

3. systematyczne zmiany powtarzające się co kilka lat

7) Dominanty (Modalnej) nie wyznaczamy gdy:

1. szereg jest bimodalny

2. przedziały klasowe są równej rozpiętości

3. szereg jest symetryczny

4. granice przedziałów są otwarte

8) Spis powszechny jest badaniem:

1. częściowym

2. ciągłym

3. jednorazowym

4. całkowitym

5. umożliwiającym szacowanie stanów i struktur ludności w okresach między spisami

6. umożliwiającym wypełnienie luk w materiale statystycznym

9) Trend to:

1. wahania wywołane wzrostem badanego zjawiska

2. ogólna tendencja rozwojowa

3. wahania cykliczne

10) Które szeregi są utworzone według kryterium merytorycznego? (czyli wg treści)

1. czasowe = TREŚĆ

2. rozdzielcze = FORMA

3. strukturalne = TREŚĆ

4. skumulowane

5. przestrzenne = TREŚĆ

---