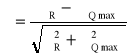
Wykorzystane wzory:

Wartości: σ_max, μ_max, R_n obliczono jak w zadaniu 8.

1,0⋅D+1,5⋅L+1,0⋅S+1,0⋅W=

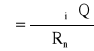
μ_R = λ_R X_R

σ_R = V_R μ_R

Wariant 1:

	częst.	D	L	W	S	mmax	s^2max	mR	Rn	FRn	F	Rn F=0,75	mR	sR	b
1	rzadko	40	40	10	10	84	72,508	155,967	135,62	120	0,885	160	184	22,08	4,226
2	rzadko	20	60	10	10	83	124,078	161,085	140,07	130	0,928	173,333	199,333	23,92	4,409
3	często	30	20	50	0	77,3	133,292	153,324	133,33	110	0,825	146,667	168,667	20,24	3,921
4	często	30	20	0	50	75,3	216,778	159,976	139,11	110	0,791	146,667	168,667	20,24	3,730
5	często	20	80	0	0	101	211,770	198,807	172,88	140	0,810	186,667	214,667	25,76	3,842
	gamma	1	1,5	1	1

Przyjęcie F=0,75 pozwala na osiągnięcie współczynników bezpieczeństwa >3,5 dla wszystkich kombinacji

Przyjęcie F=0,8 spowodowało by obniżenie współczynnika bezpieczeństwa poniżej wymaganego 3,5 w przypadku kombinacji występującej często (kombinacji 4)

Przyjęta wartość wskaźnika  spowodowała wzrost współczynnika niezawodności  powyżej zakładanego poziomu 3,5. Dla niektórych przypadków wartość ta został znacznie przekroczona dlatego. Można dopuścić taką możliwość gdyż przypadki te występują rzadko. Można także spróbować przyjąć dwa różne współczynniki  dla przypadków

Wariant 2 - różne :

	częst.	D	L	W	S	mmax	s^2max	mR	Rn	FRn	F	Rn F=0,85	mR	sR	b
1	rzadko	40	40	10	10	84	72,508	155,967	135,62	120	0,885	141,176	162,35	19,48	3,685
2	rzadko	20	60	10	10	83	124,078	161,085	140,07	130	0,928	152,941	175,882	21,10	3,892
												F=0,75
3	często	30	20	50	0	77,3	133,292	153,324	133,33	110	0,825	146,667	168,667	20,24	3,921
4	często	30	20	0	50	75,3	216,778	159,976	139,11	110	0,791	146,667	168,667	20,24	3,730
5	często	20	80	0	0	101	211,770	198,807	172,88	140	0,810	186,667	214,667	25,76	3,842
	gamma	1	1,5	1	1

Przyjęcie dwóch różnych współczynników  powoduje zmniejszenie współczynnika niezawodności występującego w przypadku 1 i 2. Prowadzi to jednak do znacznej komplikacji obliczeń. Ponieważ poprawia to jedynie sytuacje w przypadkach występujących rzadko dlatego uważam iż powinno się przyjąć jeden współczynnik dla wszystkich przypadków F=0,75.

Zadanie 9 - Anna Pszczółkowska

_____________________________________________________________________

nowe wartości współczynnika

b

4,2

4,4

3,9

3,7

3,8

3,5

3,5

3,5

3,5

3,5

3,0

3,2

3,4

3,6

3,8

4,0

4,2

4,4

4,6

0

1

2

3

4

5

6

przypadek



nowe wartości współczynnika

b

3,7

3,9

3,91

3,7

3,8

3,5

3,5

3,5

3,5

3,5

3,3

3,4

3,5

3,6

3,7

3,8

3,9

4,0

0

1

2

3

4

5

6

przypadek



---