POLITECHNIKA ŚLĄSKA

W GLIWICACH

WYDZIAŁ ELEKTRYCZNY

WYZNACZANIE ŁADUNKU WŁAŚCIWEGO e/m METODĄ MAGNETRONOWĄ .

WPROWADZENIE.

Postulat istnienia ładunku elementarnego został potwierdzony doświadczalnie na przełomie ubiegłego wieku . Najpierw J.J.Thomson wykazał podczas eksperymentów z promieniami katodowymi , że stosunek ładunku do masy cząstek stanowiących te promienie jest stały i wynosi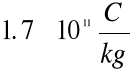
. Natomiast sam ładunek elementarny wyznaczył R.A.Millikan .

Do wnętrza płaskiego kondensatora wprowadza się rozpylone kropelki oleju . Opadanie kropelki oświetlonej światłem bocznym obserwuje się za pomocą lunetki z okularem metrycznym . Znając prędkość opadania oraz dane materiałowe ośrodka i oleju można wyznaczyć promień kropli . Następnie kroplę jonizujemy stosując np. lampę rentgenowską . Znając prędkość przemieszczania się naładowanej kropli w obecności pola elektrycznego wewnątrz kondensatora można wyznaczyć wartość ładunku .

Millikan wykazał , że ładunek kropli jest całkowitą wielokrotnością ładunku elementarnego
.

W naszej pracowni stosujemy metodę magnetronową wyznaczania ładunku właściwego e/m .

Opis zestawu pomiarowego .

Indukcja magnetyczna w środku solenoidu określona jest wzorem ;

gdzie
- przenikalność magnetyczna próżni ,

I - natężenie płynącego prądu ,

n - liczba zwojów przypadająca na jednostkę długości cewki .

Zależność między indukcją magnetyczną a natężeniem prądu wyrazimy wzorem empirycznym :

gdzie - współczynnik zależny od geometrii cewki , liczby warstw , liczby zwojów w warstwie . W przypadku cewki stosowanej w zestawie
.

Ładunek właściwy e/m obliczymy ze wzoru :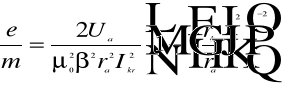

Przebieg ćwiczenia.

1.Łączymy obwód wg schematu :

2. Przy ustalonym napięciu anodowym ( np.6v ) notujemy zmiany natężenia prądu anodowego
spowodowane zmianą natężenia prądu płynącego przez solenoid I . Natężenie prądu I zmieniamy w granicach

0 - 1500 mA co 100 mA .

3. Podobne pomiary przeprowadzamy przy trzech różnych wartościach napięcia anodowego np. 6 , 8 , 10 V .

4. Rysujemy rodziny charakterystyk

5. Z wykresów określamy wartości krytyczne
prądu płynącego przez solenoid odpowiadające dwukrotnemu spadkowi prądu anodowego ( w porównaniu z wartością początkową przy I = 0 ) .

6. Obliczamy ładunek właściwy e/m :

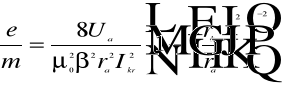
gdzie :
- promień anody ,

- promień katody ,

- stała aparaturowa zależna ad geometrii cewki ( rozmiarów , liczby zwojów , liczby warstw uzwojenia ) .

7. Obliczamy średnią ważoną ładunku właściwego e/m .

8. Przeprowadzamy rachunek błędów .

TABELA POMIAROWA .

MIERNIK	KLASA [%]	ZAKRES	DOKŁ.ODCZYTU
Woltomierz	0.2	15 V	0.08 V
Miliamperomierz	0.2	30 mA	0.2 mA
Miliamperomierz	0.2	1500 mA	10 mA

TABELA POMIAROWA .

100	32.5	27.4
200	32.5	27.2
300	32	26.8
400	31.5	26.4
500	31	26
600	30.5	25.2
700	28.6	23.6
750	25.6	20.6
800	22.2	17.2
850	18.6	14.4
900	15.8	12.2
950	13.2	10.2
1000	11.4	9
1100	9	7.2
1200	7.2	5.8
1300	6	4.8
1400	4.8	3.8
1500	4	3

TABELA POMIAROWA .

30	17
120	17
200	16.8
290	16.6
320	16.5
400	16.3
440	16.2
490	16.1
540	14.8
650	14.2
660	13.2
690	10.2
750	8
820	6.9
860	6.3
890	5.5
940	4.7
1000	4.2
1050	3.8
1090	3.4
1150	3
1220	2.4
1300	2
1400	1.8

TABELA POMIAROWA .

30	12.8
100	12.8
200	12.6
300	12.4
400	12.2
500	12
560	11.7
600	11.3
650	10.2
660	9.6
680	9.1
710	8.2
740	7
800	5.6
850	4.7
900	4.2
940	3.6
990	3.2
1050	2.8
1100	2.6
1150	2.3
1210	2
1300	1.6
1400	1.4
1480	1.2

Z wykresu określamy wartości krytyczne prądu płynącego przez solenoid

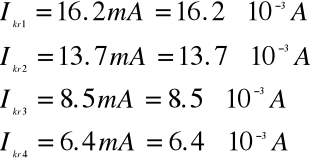
Obliczamy ładunek właściwy e/m .

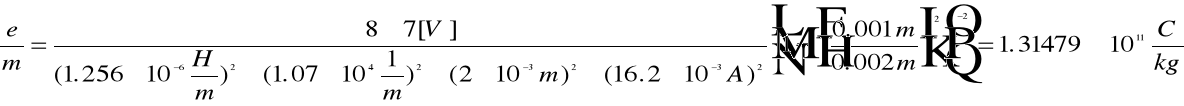
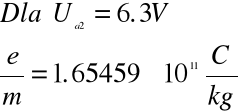
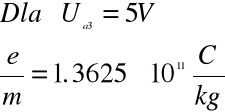
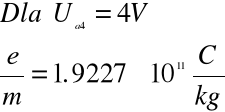
Obliczamy błąd wielkości złożonej metodą różniczki zupełnej .

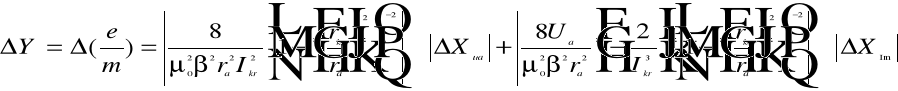
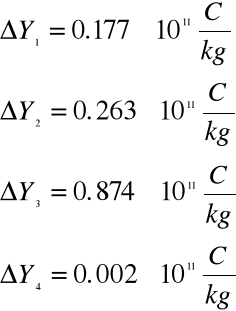
Obliczamy średnią ważoną wartość ładunku właściwego e/m .

Wartość średnia ważona = 1.923098791323241E-011

Błąd maks. średniej ważonej = 2.008344144566105E-012

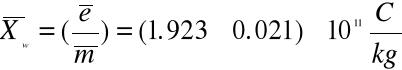
Wnioski .

Zwiększając prąd cewki obserwujemy gwałtowny spadek prądu anodowego . Dzieje się tak dlatego, że na wyemitowane przez katodę elektrony, poruszające się z prędkością [v] działa prostopadle pole magnetyczne o indukcji [B] spowodowane przepływem prądu przez nawiniętą wokół lampy cewkę. Pojawia się wtedy siła, prostopadła do chwilowej wartości prędkości elektronów, powodujaca zakrzywienie ich trajektorii.Elektrony zataczają łuk, a siłę działającą na nie można nazwać dośrodkową. Ta sama siła sprawia, że elektrony nie "trafiają" do anody,

a lampa staje się "rezystorem".

Reasumując: Wzrost prądu w cewce wywołuje wzrost indukcji magnetycznej, która ma wpływ na wzrost siły Coriolisa. Ta z kolei oddziaływuje na przepływające w lampie elektrony, które "rozwierają" obwód anody. Wpływ siły jest tym większy im mniejsza jest masa elektronów.

---