63284

Równanie Bernulliego (Ma cieczy lepkiej.

Dla stiugi

P\ ^Vl    P' ^V2 Tl

dla strumienia

-_łfl._ł!Ł.,_lł£Ł_ł!Ł_łr

r 2_g ² , 2_g ^L ■"

Zi,Z; -wzniesienie linii prądu ponad poziom porównawczy

— -wysokość ciśnienia (ciśnienie panujące w danym piuikcie linii prądu wyrażona za

pomocą wysokości słupa rtęci)

V*

— -wysokość prędkości 2g

v -prędkość średnia

« - wsp. de Sant Venant’a

3) Wsp. strat według Nikuradsego . Bezwymiarowy wsp oporów /. .

Zależy od:

-lepkości cieczy

-rodzaju ruchu(czyli liczby Reynoldsa ) -względnej chropowatości przewodu

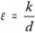
k- bezwzględna chropowatość d- średnica przewodu Wyróżnia się zakresy:

64

I    - ruch lammamy ^{ł =} 'dT

II    - strefa przejściowa

III-    X - 0,316    ⁰¹²⁵

IV-    >. osiąga płytki minimum

V - /. zależy tylko od chropowatości względnej