65472

ki

tensor krzywizn powierzchni środkowej

Równania fizyczne zapisać dla "k-tej" warstwy laminatu ma postać:

°v	=[q],		-łjęlkZ-	*3 ^Kv
^Txy.	k	vSy		KT° ^xy

Uwzględniając liniową zmianę odkształceń po grubości laminatu i fakt, że sztywności warstw go tworzących są z reguły różne, otrzymuje się to rozkłady odkształceń i naprężeń po grubości laminatu jak na rysunku

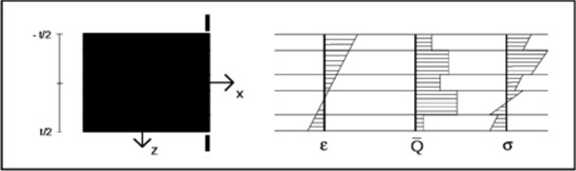
Przykładowy rozkład naprężeń po giubości laminatu.

Wypadkowe siły i momenty w laminacie

Naprężenia w laminacie określa się jako wielkość uśrednioną naprężeń warstwowych po grubości laminatu

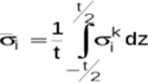
gdzie ^<rT oznacza "i-tą* składową naprężenia średniego w laminacie, <r-p- - "i-tą" składową naprężenia w "k-tej" warstwie laminatu, zaś t jest grubością laminatu.

Siły ł momenty wypadkowe (siły i momenty na jednostkę szerokości przekroju.

i= Jcf zdz

N

= C_t= Jof

-yś.

dz

M

Wypadkowe siły i momenty dla laminatu można przedstawić w postaci

Nx]		^A11	A12	A16	^e°		Bu	B12	Bi6	[^K°]
Ny	=	A12	A 22	A 26	^£y	4	B12	B 22	B26	^Ky|
		_A 16	A 26	A 66 _	A.		B16	B 26	^b^,^6J
Mx		Bn	B12	B 16	eS		Dn	Di2		! ntetr
My		B12	B22	B26	e?	-ł	Du	D22	d26	UJ
M xy		_B 16	B 26	^B66 _	A		^D16	^D26	Avs ^U66_	5™gtr ^Kxy

fczna macierz sztywności tarczowej

Macierz Bij wywołuje sprzężenie stanu tarczowego i giętnego w laminacie. Tak więc w ogólnym przypadku laminatu o całkowicie dowolnej budowie - stanom tarczowym (dla przykładu siła skupiona działająca w płaszczyźnie laminatu) towarzyszą stany giętne (zginanie, zwichrzenie) i odwrotnie.

2