88464

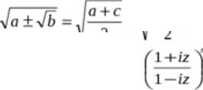
6)    a) Znaleźć wszystkie zespolone pierwiastki stopnia 5 z jedynki, rozwiązując równanie

± J^a ^ ^C, gdziec‘ = a‘

5)    Znaleźć wszystkie zespolone rozwiązania równania

z^J + z³ + z² + z +1 = 0, po podzieleniu przez z², za pomocą podstawienia z + — = w. Znaleźć także pierwiastki

z

piątego stopnia z liczb -1, i oraz -i.

b) To samo, korzystając z tego, że 3*72=360 - 2*72, sin 3x = 3 sin x - 4 sin³x.

Rozwiązać w ciele liczb zespolonych równanie:

a)    (z² +1)² -(z² -l)² =4(1 + 2>/2i)

b)    (z² +1)² -(z² -l)² =4(1 + V3i)

Rozwiązać w liczbach zespolonych równanie z^l-i)⁴.

Obliczyć wszystkie możliwe wartości wyrażenia: ^1 + cos^+sin    j .

Rozwiązać w ciele liczb zespolonych równanie (z + 2)³ — (z + l)³ — 9z = 4. Rozwiązać w ciele liczb zespolonych równanie (z + l)² + (z -1)² = 2(2 + i). Rozwiązać w ciele liczb zespolonych równanie z — z³-

Obliczyć pierwiastki

(1+730’ (73-O¹

. /(-l + o²⁶

¹,c^fc3^r

Obliczyć

Uwaga. Przy obliczaniu pierwiastków kwadratowych z liczb zespolonych niekiedy są przydatne tożsamości

b.

⁼y^±^r-gdzi ec² = fl‘

Rozwiązać równania: a) z³ + l = 0;b) _z* +4 + 4/>/3 = 0; c) 8>/2z³+1-/= 0-

Obliczyć

V3+l+(V3-l)i

2+2/

r

oraz Im

ĆV3+1+(V3-1)/ T

2+2/

Obliczyć wszystkie zespolone pierwiastki równania z⁵ = z

Granice: ciągłość funkcji.

1. Obliczyć granice, o ile istnieją:

..    x + sinx    ,    VT*

a) lim    ^L'^,!- ¹

x-*»x-sinx

b) lim

x—>0

■vr

c) lim

Jx -6

5y[x

d)lim

e) lim

yJx-Jx + ^< V2x+1

f) lim x-»0

sin(l/x)

g) lim x(— 2

arc tgx) h) lirn

■J3 + 2x -V3-2x Tc 12-arcsin x