5466967423

95. Znaleźć wszystkie rozwiązania równania — = |x|.

96.    Duży garnek świeżo ugotowanej zupy o temperaturze 100° C chłodzony jest w bieżącej wodzie o temperaturze 5° C; zupa jest mieszana, więc można przyjąć, że jej temperatura jest taka sama we wszystkich punktach garnka. W ciągu 10 minut temperatura zupy obniżona została do 60° C. Zakładając, że obowiązuje prawo stygnięcia Newtona (szybkość zmniejszania się temperatury układu jest proporcjonalna do różnicy temperatur między układem a otoczeniem), obliczyć, w jakim czasie garnek ostygnie do temperatury 20° C.

97.    Wykazać, że jeśli funkcja /: Rⁿ —► Rⁿ spełnia warunek Lipschitza, to rozwiązania równania Tif = f(x) są określone dla wszystkich te R.

98.    Rozwiązać równanie x' + 2tx — e~^ł sin t.

99.    Rozwiązać równanie tx' — 1 + x².

100.    Rozwiązać równanie tx' = a;(lna; — lnt).

101.    Rozwiązać równanie x' =    .

102.    Niech A będzie funkcją ciągłą określoną na przedziale (a, b), a < b, której wartościami są macierze wymiaru n x n. Udowodnić, że zbiór rozwiązań układu równań x' = A(t)x jest przestrzenią liniową. Znaleźć jej wymiar.

103.    Obliczyć exp(L4), jeśli

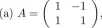
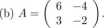
104. Macierz

ma dokładnie dwie różne wartości własne, obie nierzeczywiste, jej wyznacznik jest równy 25. Rozwiązać układ równań liniowych jednorodnych x' = Ax.

105. Rozwiązać układ równań liniowych jednorodnych x' = Ax, jeśli

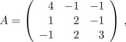
wiedząc, że jedną z wartości własnych macierzy A jest liczba 3, dwie następne nie są rzeczywiste, a wyznacznik A jest równy 30.

106. Udowodnić, że dziedzina każdego rozwiązania układu równań

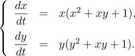
zawiera półprostą (—oo, 0] oraz że każde rozwiązanie tego układu spełnia warunek

,1'IPoo W⁴)^{2 +} »M²) ⁼ °-

107. A jest macierzą wymiaru n x n, której wszystkie wartości własne mają ujemne części rzeczywiste. Funkcja x : R —* Rⁿ jest dowolnym rozwiązaniem układu: x'(t) = Ax(t). Udowodnić, że ^lim x(t) = 0.