89697

Chemia I sem. M. Twardowska, uzup. WZ Równania różniczkowe. 2

drugiego warunku (F' = Q) dostajemy pewne równanie na pochodną funkcji ^p(y) czyli ^(y), przy czym bardzo istotne jest że owa pochodna, podobnie jak sama funkcja <p(y) może zależeć tylko od zmiennej y (inaczej mówiąc, wszystkie człony zawierające zmienną x muszą się zredukować). Jeżeli tak nic jest, tzn. wychodzi nam, że tf(y) i w konsekwencji samo <f(y) zależy nic tylko od zmiennej y. ale i od x - może to oznaczać albo że samo badane równanie nie jest równaniem zupełnym albo że nastąpi! błąd przy jednym z całkowań. Aby wykluczyć takie pomyłki, dobrze jest bezpośrednio sprawdzić, czy warunek konieczny zupełności równania jest spełniony.

G. Jeżeli P(x,y)dx + Q(x,y)dy = 0 niekoniecznie jest równaniem zupełnym, ale |>o pomnożeniu przez /x(ar, y) powstałe równanie czyli /i(x, y)P{x, y)dx+fi(x, y)Q(x, y)dy — 0 jest równaniem zupełnym, to funkcję fi(x,y) nazywamy czynnikiem całkującym lub mnożnikiem całkującym dla tego równania. YV ogólnym przypadku, znalezienie mnożnika całkującego dla równania wymagałoby rozwiązania pewnego równania różniczkowego o pochodnych cząstkowych, co jest na ogół jeszcze tnidniejsze niż rozwiązanie pierwotnego równania, ale w szczególnym przypadku gdy istnieje czynnik całkujący zależny tylko od jednej zmiennej (x albo y), to można go znaleźć stosunkowo łatwo, a mianowicie:

~i(S

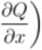
zależy tylko od zmiennej x, to równanie ma czynnik całkujący

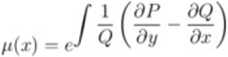
(Lr

jeśli

l(OQ

p\dx

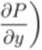
zależy tylko od zmiennej y. to równanie ma czynnik całkujący

p(y) =

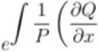
op\

Oy)

dy

Rozwiązać równania różniczkowe:

1)    (o rozdzielonych zmiennych):

») Sr ^{= e2X+W;} xy'^{+ y =} c) Wra- + ydy = 0: d) {y² + xyⁱ)dx + (x² - x²y)dy = 0.

2)    (jednorodne względem x i y)

a) = * ^+y-; b) y- = * ^{+ !J} ;    c) y² + x*if = d) (y² -3x²)dy+ 2xydx = 0;

dx xy    dx 3x-y

e)(x²+2xy-y²) + (y² + 2xy-x²)y' = 0; f)'y¹ - xi/= x + g) (2x - y)tj = 2y - x.

Vl/\

3)    (liniowe): a) — ytgx = 2sin j-; b) xf + — = x²\ c) i/ + 2xy = e ^x‘: d) y' — 2xy = 2x³:

dx    x

1 _ 2x

^e) l/ + Vcosa: = sinzeoss; f) i/ — e*y = e²*: g) t/ H---—y = 1, j/(l) = 1 + e.

3y/ź

y² ;

x¹

4)    (Bernoulliego): a) ry* + xy² - y = 0: b) \J + xy = xy~³: c) y^ + \y = d) y^ + - =

(lx o y/y (tx x

e) -y: + \Xy/y = 2ze~^x’; f) y' - 9x²y = (z⁵ + x²)y^2,3\ g) y' - 9x²y = 3(z⁵ - x²)y^2/3.

Vy

5)    (zupełne - sprawdzić!)