96131

TWIERDZENIE LIOUVILLE’A O KWADRATURACH

Załóżmy, że iiklad hamiltonowski ma n stałych ruchu F|(q,p), F2(q.p).....F_n(q.p). gdzie

F|(q,p)=H(q,p). Załóżmy, że stałe są niezależne i w inwolucji. Wówczas:

-    trajektorie q(t), p(t) układu leżą na rozmaitości niezmienniczej

M,={(q.p)eR²ⁿIF|(q.p)=f|.....F_n(q.p)=f_n} o wymiarze n.

-    Trajektorie g(t), p(t) można wyznaczyć przez kwadratury.

*) Niezależność:

			BF\	dF\ dF\	dF\
	(lF\(q,p)		dq\	dqn ' dp\	dPn
rani	dFn(q,p)	= ran A	dF„	dF„ . dF„	dFn
			dq\	dąn ^dP\	ć>Pn

*) Rozmaitość: k-wymiaiowa jest to zbiór rozwiązań m niezależnych równali o n niewiadomych ( k=n-m)

*) Inwolucja : {Fi.Fj)=0

Twierdzenie Liouville’a o dywergencji

Jeżeli div f(x)=0 to strumień pola zachowuje objętość, tzn. dla ^6,6 dńfot M)= dh(o)

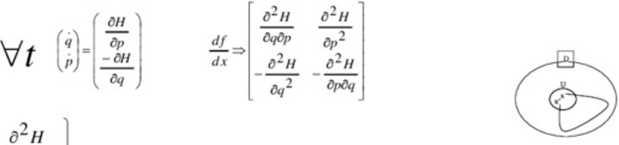
dqjdpj

d²H

zachowuje pole

dpjdc/j

Układ równań kanonicznych hamiltona ma dywergencję równą 0.

Twierdzenie Poincare’go powrocie

Załóżmy, że układ dynamiczny x’=f(x) ma divf(x)=0,oraz, ż D € IR“ jest ogr aniczonym zbiorem niezmienniczym tego układu (x€ D=> <p,(x) e D) Wówczas, dla każdego x e D, dla każdego otoczenia otwartego U punktu x istnieje x € U i chwila t>0, tak że (p,(x) e U