0239

241

§ 2. Zbieżność szeregów o wyrazach dodatnich

Kryterium Bertranda. Załóżmy, że ciąg {^CX3_I1} ma skończoną lub nieskończoną granicę

T3 = lim °8_m .

Wó wczas jeśli ^CB> 1, to szereg jest zbieżny, jeżeli zaś ‘OS < 1, /o jest rozbieżny.

(1 \^l,+1

1 + ~ I = ln e = 1, ciąg Kummera jest zbieżny do granicy

% = ^CB— 1 (X = db oo, jeżeli ^CB = ± oo).

Pozostaje powołać się na kryterium Kummera.

Porównując ze sobą kryterium Raabego i Bertranda, można by powtórzyć te same uwagi, które zrobiliśmy wyżej w związku z kryteriami d’AIemberta i Raabego [369]. Łańcuch takich coraz czulszych (lecz jednocześnie coraz bardziej skomplikowanych) kryteriów można przedłużyć nieograniczenie.

372. Kryterium Gaussa. Z kryteriów d’Alemberta, Raabego i Bertranda łatwo można otrzymać następujące kryterium C. F. Gaussa:

Kryterium Gaussa. Załóżmy, że dia danego szeregu (A) stosunek aja_n+1 można przedstawić »*’ postaci

-JLu-^I+JL + Źl, a„+i    n ir

gdzie X i /< są stale, a O.jest wielkością ograniczoną: |0„|<I.. Wówczas szereg jest zbieżny, jeżeli A>1 lub jeżeli X — 1 / /i >1, i jest rozbieżny, jeżeli 1< 1 lubjeżeliX— 1 ifi< 1.

a.+ t _ 1

Przypadki X> 1 i A< 1 sprowadzają się do kryterium d’Alemberta, bo lim ^——--. Niech teraz

1 = 1. Wówczas

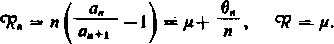
W przypadku p>\ lub p< 1 sprawę rozstrzyga kryterium Raabego. Jeśli wreszcie p = 1, to jest

9?„ = Inn (<7?.-!) = — U..

n

Ponieważ dąży jak wiadomo, do zera, gdy » -*• oo, a 0* jest ograniczone, więc U = lim ^CB« = 0 i na mocy kryterium Bertranda szereg jest rozbieżny.

Przykłady. 1) Rozpatrzmy tzw. szereg hipergeometryczny (Gauss).

F(x, P,Y,x)

OO

■(«+!)• ... -(a+n-n-ZH/i+l)- ... -Ut+n-1) ^

n! y(y+ !)• ... -(y+n-1)

= 1 +

1-2

*+

a-(oH-l)/H/H-l)    -    «-(a+l)-(<x+2)-ft-(ft4-l)(/?+2)

l*2*y(y+l)    '    l-2-3-y(y+l)-(y+2)

*³+

zakładając na razie, że ot, fi, y, x>0. Tutaj

a.+t _ (a + n)(P+n) a. ~ (1 +n) (y+n)

a więc na podstawie kryterium d’Alemberta od razu stwierdzamy zbieżność szeregu dla x<l i rozbież-16 Rachunek różniczkowy