0237

239

§ 2. Zbieżność szeregów o wyrazach dodatnich

371. Kryterium Kummera. Podamy teraz pewne bardzo ogólne kryterium należące do E.E. Kumme-ra; należy je raczej uważać za ogólny schemat otrzymywania różnych konkretnych kryteriów.

Kryterium Kummera. Niech

^li ^ 2» • * *» ^*«» • ■ •

będzie takim dowolnym ciągiem liczb dodatnich, że szereg

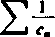
jest rozbieżny (‘). Utwórzmy dla szeregu (A) ciąg o wyrazach

a«+i

Jeżeli dla n>N jest spełniona nierówność

^.>6,

gdzie 6 jest stalą liczbą dodatnią, to szereg jest zbieżny, jeżeli zaś (dla n > N) jest

9C, <0.

to szereg jest rozbieżny.

Dowód. Niech będzie

9C. = c„-^- -r„₊i > <5 > 0 ;

tffi + I

możemy oczywiście przyjąć, że nierówność ta jest spełniona dla wszystkich n.

Mnożąc obie strony tej nierówności przez a„_+l otrzymujemy

(6) c_na_n — c_n+i fl„ + i < d'a_ą + i ,

a więc

c. fl„-c„+i «„+! > 0 , czyli c_n a„ > c„₊₁ a„₊₁ .

Wynika stąd, że zmienna c„a„ maleje monotonicznie, a zatem dąży do skończonej granicy (gdyż jest ograniczona z dołu przez zero). Tak więc szereg

J](c.o„-c.₊₁a.₊₁)

n>l

jest zbieżny, bo suma n jego pierwszych wyrazów równa

Ci a_t — c„+i cr„ + i

ma granicę skończoną. Ale wówczas z nierówności (6) wynika na mocy twierdzenia 1, że zbieżny jest

szereg ^da.+i, a wraz z nim dany szereg (A).

*■1

Jeśli zaś dla n > N jest

9T„=c,-^--c„₊₁ <0,

a„+1

(') Zwracamy uwagę czytelnikowi, że z tego ostatniego założenia będziemy korzystali tylko przy wyprowadzeniu kryterium rozbieżności, dla kryterium zbieżności nie jest ono potrzebne.