1 (57)

63

Zbieżność bezwzględna

3.46. Uwagi. Dla szeregów o wyrazach dodatnich zbieżność bezwzględna jest tym samym, co zbieżność.

Jeśli szereg ]T a„ jest zbieżny, a szereg ]T \a_n\ jest rozbieżny, to mówimy, że szereg £ a_n jest zbieżny warunkowo. Na przykład szereg

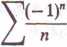
jest zbieżny warunkowo (twierdzenie 3.43).

Kryterium porównawcze, jak również kryteria d’Alemberta i Cauchy’ego, są w rzeczywistości kryteriami zbieżności bezwzględnej i dlatego nie dają żadnych informacji o zbieżności warunkowej szeregów. Sumowanie częściowe może czasami służyć do rozpatrywania tych ostatnich. W szczególności szereg potęgowy jest bezwzględnie zbieżny wewnątrz koła zbieżności.

Zobaczymy, że z szeregami bezwzględnie zbieżnymi można postępować tak, jak z sumami skończonymi. Można je wymnażać członami i przestawiać składniki nie zmieniając sumy. Dla szeregów zbieżnych warunkowo to już jednak nie zachodzi i przy wykonywaniu działań na nich konieczna jest ogromna ostrożność.

Dodawanie i mnożenie szeregów

3.47.    Twierdzenie. Jeśli £a„ = A i = B, to £(«„+&„) = A+B i £ca„ = cA dla dowolnego ustalonego c.

n    n

Dowód. Niech A„ = £ a_k, B„= £ Ąt-Wówczas *=q    *=o

n

A„+B_n = Y, (<%+W*

*=o

Ponieważ lim A_n = A i lim B„ = B, widzimy, że lim (A„+B„) = A+B.

n~* oo    n-+ oo    u** oo

Udowodnienie drugiej równości jest jeszcze łatwiejsze.

Dwa szeregi zbieżne można więc dodawać wyraz do wyrazu i otrzymany szereg będzie zbieżny do sumy sum tych dwóch szeregów. Sytuacja komplikuje się w przypadku rozpatrywania iloczynu dwóch szeregów. Najpierw powinniśmy zdefiniować iloczyn. Można to-zrobić na wiele sposobów; będziemy rozpatrywać tak zwany iloczyn Cauchy’ego.

3.48.    DEFINICJA. Weźmy dwa szeregi i i przyjmijmy

n

C„ = £ ^a*^bn-k (n - O, % 2,...).

k= O

Szereg £ c„ nazywamy iloczynem dwóch danych szeregów.

Definicję tę można objaśnić w następujący sposób. Jeśli wziąwszy dwa szeregi potęgowe-