3784494694

na ż-tym miejscu jedynkę. Dowolne różne elementy a i b zbioru S mają wówczas przypisane różne numery, które różnią się, powiedzmy, na j-tym miejscu. Wtedy do zbioru Aj należy dokładnie jeden z elementów a, b.

Tak znaleziona liczba k jest najmniejsza. Załóżmy bowiem, że istnieją zbiory Ai,A2,...,Ak spełniające warunki zadania dla 2^k <n. Każdemu elementowi x zbioru S przypisujemy układ k liczb (ci,C2,...,Cfc) według następującej zasady:

f 0 gdy x £ Ai 11 gdy x e Ai

Ponieważ 2^fc < n, więc istnieją dwa różne elementy a,&E S, które mają przypisany ten sam układ liczb. To zaś oznacza, że element a należy do dokładnie tych samych zbiorów spośród A\,A2,...,Ak, co element b.

Zadanie 9. Punkty D, E, F leżą odpowiednio na bokach BC, CA, AB trójkąta ABC. Okręgi wpisane w trójkąty AEF, BFD, CDE są styczne do okręgu wpisanego w trójkąt DEF. Udowodnić, że proste AD, BE, CF przecinają się w jednym punkcie.

Rozwiązanie Sposób I

Rozwiązanie to opiera się na twierdzeniu mówiącym o tym, że złożenie dwóch jednokładności jest (na ogół) jednokładnością. Dokładne sformułowanie tego twierdzenia oraz jego dowód znajduje się na końcu niniejszej broszury (zob. Dodatek, „Twierdzenie o złożeniu jednokładności”, str. 114).

Niech K, L, M będą odpowiednio punktami styczności okręgu wpisanego w trójkąt DEF z bokami EF, FD, DE (rys. 1). Przyjmijmy ponadto, że okrąg wpisany w trójkąt AFE jest styczny do boków EF, FA, AF odpowiednio w punktach K, P, Q. Wówczas ME — KE — QE oraz LF = KF = PF. Stąd otrzymujemy

AF + DE = AP+PF+DM + ME = AQ + QE+FL+LD = AE+DF.

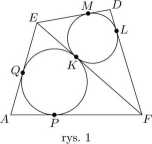
Udowodniliśmy więc, że jeśli okręgi wpisane w trójkąty AFE oraz DEF są styczne, to w czworokąt AFDE można wpisać okrąg. Oznaczmy ten okrąg przez oa-

41