3784495606

102 15. Elementy teorii uczenia się w grach

pewną strategią mieszaną, którą definiuje następująco. Prawdopodobieństwo każdej dostępnej strategii czystej każdego z pozostałych graczy jest równe częstości dotychczasowego jej używania przez tego gracza. W kolejnej rundzie "uczący się” gracz wybiera najlepszą odpowiedź na tak zdefiniowany profil strategii mieszanych gry.

W przypadku dwuosobowych gier strategicznych procedura gry fikcyjnej zakłada że gracz zapamiętuje wszystkie grane przez przeciwnika strategie czyste (historię gry) i na jej podstawie tworzy rozkład prawdopodobieństwa grania przez przeciwnika poszczególnych strategii czystych-strategię mieszaną-w następnej rundzie, w której gra najlepszą odpowiedź na tę strategię mieszaną.

Można pokazać że w przypadku gry z więcej niż jednym przeciwnikiem, przy założeniu że gracz będzie przewidywał rozkład łączny, finalnym efektem procedury jest na ogół równowaga skorelowana.

Dla wielu typów gier procedura gry fikcyjnej jest zbieżna to równowagi Nasha. Istnieją jednak proste kontrprzykłady, związane z brakiem ciągłości odwzorowania najlepszej odpowiedzi, z których pierwszy był skonstruowany w pracy [32]. Metody "uzbieżniania” procedury polegają na wprowadzeniu różnych typów niedużych zaburzeń do gry, lub rozważanie populacji graczy zamiast jednego, patrz [26].

Równowaga Nasha została wprowadzona w 1950 r. Rok później zostały zaproponowane algorytmy znajdowania równowag Nasha. Algorytmy te zostały później zinterpretowane jako modele uczenia się w grach, w szczególności jako procedury gry fikcyjnej patrz np. [2, 27].

15.3.4.    Uczenie się przez testowanie

Gracz rozgrywa z przeciwnikiem |Sj gier jednokrotnych, używając kolejno wszystkich dostępnych mu strategii czystych, i używa do gry tę która mu dała największa wypłatę (w przypadku kilku takich strategii wybiera losowo jedna z nich). Ta procedura nosi nazwę procedury jednokrotnego testowania. Przy k-krotnym powtórzeniu takiego algotytmu n-krotnego otrzymujemy procedurę k-krotnego testowania, por. [18]

15.3.5.    Procedury porównań

Powyższe modele uczenia się można uogólnić na jeden model który nazwiemy modelem porównywania ([25]).

Załóżmy że gracz gra pewną strategią i. Dokonuje sie w pewien sposób (losowy lub nie) wyboru pewnego elementu u> € fi (lub zbioru elementów) który nazwiemy próbką. Próbka służy graczowi do porównania strategii i wyboru-z pewnym prawdopodobieństwem-jednej z nich.

Wyjściowym formalnym obiektem modelu jest rodzina przestrzeni probabilistycznych < Q,B,P >, gdzie zbiór próbek jest metryzowalna przestrzenią topologiczną, B jest cr-algebrą zbiorów Borelowskich, a P jest zbiorem wszystkich miar probabilistycznych na B.

Próbka u jest losowana zgodnie z pewnym rozkładem jieP. Prawdopodobieństwo zamiany strategii i na j jest dane wzorem

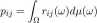
(15.7)

gdzie Tij € [0,1] jest tzw. funkcją reakcji, taką że wektor (rn(Q), ...,rj|5|(Q)) jest rozkładem prawdopodobieństwa na zbiorze strategii czystych S dla każdej strategii i € S.

W przypadku uczenia się przez imitację przestrzeń próbek jest zbiorem jednoelementowych zbiorów {i},i = 1, ...|S'|. Funkcje reakcji są takie jak w poprzednim przykładzie, ograniczonym do dwóch strategii.

Dla procedury lepszej/najlepszej odpowiedzi fi = S, tzn. przestrzeń próbek jest jednoelemen-towa, n = 1, a rij = 1/m jeżeli j jest najlepszą odpowiedzią na i, ry = 0 wpp., gdzie m jest liczbą najlepszych odpowiedzi.