3784497991

Ekstremalny element, czyli o tym, co naj... 19

jeżeli zaś zbiór D jest pusty, kładziemy

A = C, B = {«i, v₂,..., v_mj i teza zadania jest spełniona w obu tych przypadkach.

Przypuśćmy więc, że oba zbiory C, D są niepuste. Niech u będzie dowolnym zawodnikiem ze zbioru C, a u dowolnym zawodnikiem ze zbioru D. Załóżmy, że v wygrał z u. Zawodnik u wygrał, a zawodnik v przegrał spotkania z wszystkimi vi,V2, . . ■ ,v_m, otrzymujemy więc cykl v —> u —> v\ —> V2 —> ■ ■. —> v_m —> v,

który jest długości ra + 2, co stanowi sprzeczność z maksymalnością m, zatem zawodnik v przegrał z u. Skoro zawodnicy u, v byli wybrani dowolnie, dowodzi to, że każdy zawodnik ze zbioru C wygrał z każdym zawodnikiem ze zbioru D, a zatem podział A = C, B = DU{vi, V2, spełnia warunki zadania.

Zadanie 7.    Problem Sylvestera: Na płaszczyźnie dany jest skończony zbiór punk

tów o tej własności, że dowolna prosta przechodząca przez dwa punkty tego zbioru przechodzi jeszcze przez trzeci. Udowodnić, że wszystkie punkty z tego zbioru leżą na jednej prostej.

Rozwiązanie

Przypuśćmy, że punkty nie leżą na jednej prostej. Spośród wszystkich par {prosta przez dwa punkty zbioru, punkt zbioru poza tą prostą} wybieramy tę, która realizuje najmniejszą możliwą odległość punktu od prostej. Oznaczmy odpowiednio tę prostą i punkt przez l i P (patrz rysunek 3).

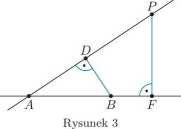
Niech F będzie rzutem punktu P na prostą Z; wówczas PF jest odległością P od l. Zgodnie z założeniem na prostej l istnieją trzy punkty naszego zbioru, zatem co najmniej dwa leżą po jednej stronie punktu F — nazwijmy je A, B, przy czym A, B, F leżą na prostej w tej kolejności (może zajść B = F).

Oznaczmy przez D rzut punktu B na prostą AP. Skoro AB ^ AF, to pole trójkąta ABP jest nie większe od pola trójkąta AFP, innymi słowy zachodzi nierówność ^4P • BD ^ AF ■ PF. Ponadto AP > AF na mocy twierdzenia Pitagorasa, więc BD < PF. To daje sprzeczność z określeniem punktu P.