3818438520

Edited by Foxit PDF Editor

Copyright (c) by Fox.it Software Company.. 2003 - 2009 For Evaluation Only,

Wykład 10: Całka oznaczona

semestr zimowy; rok akademicki 2012/2013

Połę „trójkąta parabolicznego”

Problem. Chcemy obliczyć pole s figury S ograniczonej prostą y = 0, prostą a; = 1 i wykresem funkcji f(x) = x². Rozwiązanie przybliżone. Dzielimy odcinek [0,1] na n odcinków o równej długości:

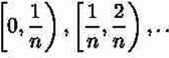
n — 1

n

,1

Suma pól prostokątów, których podstawy są równe tym odcinkom a wysokości kwadratom ich lewych końców -sensowne przybliżenie

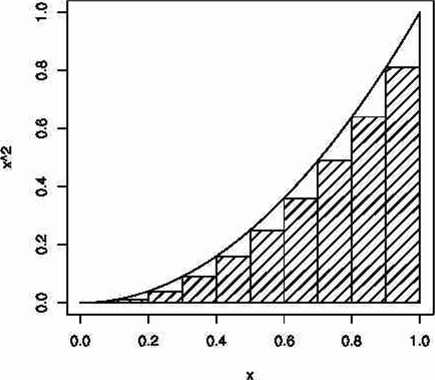
Rysunek 1: Obliczanie przybliżonej wartości pola figury S

Pole „trójkąta parabolicznego”- obliczenia

Oznaczmy pole figury odpowiadającej podziałowi odcinka na n części przez s_n. Mamy

s_n

Tl'

*=i

[n —1)»(2» — 1) 6»³

Pole figury jest równe

lim s_n = lim

«—► oo    n—>oo

(n — l)n(2n — 1) 6n³

= lim

n—>oo

2«³ — 3n² + n 6 n³

1

3

(1)

Definicja całki oznaczonej dla funkcji ciągłej

Definicja 1. Załóżmy, że funkcja f jest ciągła na przedziale [a, 6]. Całkę oznaczoną z funkcji ciągłej f na przedziale [a, 6] definiujemy wzorem

f

Ja

f{x)dx = lim

b — a

n

n ,

£/(

fc=i ^v

a + (k — 1)

b-a'

n j

(2)

1