8851785980
Rozwiązywanie równań kwadratowych
a) 9x2 — 25 = 0 korzystamy z wzoru a2 — b2 = (a + b)(a — b)
(3x + 5)(3x — 5) = 0
3x + 5 = 0 v 3x — 5 = 0 3x — —5 v 3x = 5

4x2 + 12x +9 = 0 korzystamy z wzoru a2 + 2ab + b2 = (a + b)2 (2x + 3)2 = 0 2x + 3 = 0

3
2
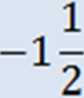
x =
Wyszukiwarka
Podobne podstrony:
Podstawy programowania - JAVAĆwiczenie 2 1. Program rozwiązujący równanie kwadratowe (zmienne
pf2 Rozdział 1 2. Określić zbiór wartości funkcji: a)/(x) = x2 - 2 + 1 Rozwiązujemy równanie kwadrat
2 ROZDZIAŁ 1. FUNKCJA WYKŁADNICZA. 1.4 Rozwiązać równania. a) r = 10 c) 9X2-7x+8
Rozwiązanie równania kwadratowego ax2 + bx + c = 0: Sub rozwiazanie_rownania_kwadratowego() rozwią
Równanie kwadratowe Liczba rozwiązań równania kwadratowego ax2 + bx + c = 0 zależy od wyróżnika
stany nieustalone str20 (130) W wyniku rozwiązania równania kwadratowego 2 R 1&nbs
Ćwiczenie 4 Płaszczyzna fazowa 1. Rozwiązanie równania kwadratowego. 2.
DSC01329 (2) 7. Algorytm rozwiązywania równania kwadratowego
MF dodatekA�26 Aneks A .7 Przybliżone metody rozwiązywania równań 271 Dla zlokalizowania pierwi
7. FUNKCJA KWADRATOWA 1. Rozwiąż równania: a) * =24 b) e) 7x‘=3,5x f> 2.
scan {y = 4 równanie kwadratowe rozwiązu- z = 8 — x jemy posług
6 (374) 25.Sposobv rozwiązywania równań bilansu wodnego -na podstawie parowania tsrenowego-oblicza s
do wymienionego wzoru podstawiamy dane z zadania rozwiązujemy równanie liniowe 30 = a, + (21 - 1) ■
294 295 (4) Rozwiązując równanie (5.43) wzglądem UMm i podstawiając uzyskany wynik do wzoru określaj
więcej podobnych podstron