9675428424

Matematyka ki o kroku
Dowód
Zauważmy, że \<AB'P\ = \<PBA'\, gd^ż kAB'P 'y£PBA są kątami wpisanymi opartymi na tym samym łuku. Także kąty <B'AP i <PA'B sąScatapu wpisanymi opartymi na tym samym luku, stąd \<B'AP\ = \<PA'B\. W konsekwencji trójkąty^+W?' i A'BP są podobne, ponieważ mają dwie pary odpowiednich kątów równych (cecha kk podobieństwa trójkątów). Otrzymujemy więc:
^r^o^\PA\.\PB\ = \PAX
1 PB'
Przykład 5.
Na prostej zawierającej średnicę AB okręgu, którego promień ma długość 14 cm, obrano punkt P w ten sposób, że odległość punktu P od środka okręgu wynosi 22 cm oraz punkt A jest punkiem wewnętrznym odcinka BP. Z punktu P poprowadzono sieczną przecinającą okrąg kolejno w punktach C i D, przy czym [ CP\ - \ CD\. Znajdź długość odcinka CD.
Oznaczmy przez x długość odcinka CD.
Z danych zadania wynika, że | PD\ = 2x.
Ponadto, ponieważ \PO\ = 22 cm, to \PA \ = 22 - 14 = 8, oraz \PB\ =22 + 14 = 36.
Z twierdzenia o odcinkach siecznych otrzymujemy równanie: x • 2x = 8 • 36. Stąd x = 12 cm.
Zadanie l.
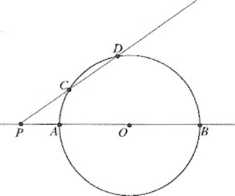
Niech t)(n. r) bidzie okręgiem o środku w punkcie O i promieniu r, a P dowolnym punktem odległym od środka okręgu o d.
Wykaż, że jeżeli PB jest sieczną przecinającą okrąg w punktach A i B, to \PA\ ■ \PB\ = \d2-r\.
Rozwiązanie
Przez punkt P i środek okręgu O poprowadźmy prostą, która przecina okrąg kolejno w punktach C i D. Rozważymy 3 przypadki.
Jeżeli punkt P leży na okręgu, to długość jednego z odcinków PA i PB jest równa zero oraz d - r, w konsekwencji \PA \ ■ \PB\ = \d2~c\ =0.
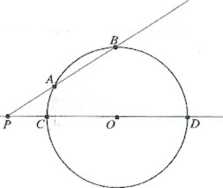
Jeżeli punkt P leży na zewnątrz koła wyznaczonego przez ten okrąg, to z twierdzenia o siecznych \PA\ - \PB\ = \PC\ ■ \PD\. Ale \PC\ =d-r,
\PD\ =d + r.
Czyli \PA\ ■ \PB\ = \PC\ • \PD\=(d-r)(d+r)=d2-i2=\d2-r2\.
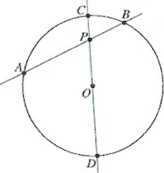
Jeżeli punkt P leży wewnątrz, kola, to także \PA\ ■ \PB\ = |PC| • \PD\. Ale \PC\ ~r-d,
\PD\ = r+d.
Czyli \PA\ - \PB\ = \PC\ ■ \PD\ = (r~d)(r + d) = r2 -d1 = \d2-- >2\.
Wytlawnictwo Edukacyjne KES POLONA Sp. z o.o., 90-743 Łódź, ul. Pogonowskiego 5/7, tel. (0-42) 636-36-34, iax (0-42) 637 38 58
3
Wyszukiwarka
Podobne podstrony:
265 § 3. Zbieżność szeregów dowolnych Łatwo zauważyć, że jeśli czynniki oc, nie rosną i są dodatnie,
M 15 A 4/2 O O 9 zauważyć, że te cztery główne ograniczenia projektowe są jednocześnie
img222 222 prostą możliwość eliminacji tych skoków. Zauważmy, że w kluczowaniu OPSK sko-ki fazy o ir
MATEMATYKA029 50 I. b tarfomoAct wstifjiiie Zauważmy, że
P3090286 Zauważmy, że wielomian interpolacyjny Lagrange a można też zapisai Yv *ki(*Kx-Xi) gdzie ir
62 (112) Matematyka. Zbiór zadań do liceów i techników. Klasa III • Łatwo zauważyć, że takich punktó
Rozwiązanie. Przyjmijmy oznaczenia: AC AB = a, ACBA = 0, ADAB = S oraz AEBA = e: C Zauważmy, że AAEB
Notatki do lekcji, klasa matematyczna - Mariusz Kawecki, IILO w Chełmie Zauważmy, że funkcja ta prze
mech2 153 304 F Zauważymy, że otrzymana wartość x Jest równa promieniowi bezwładności pręta AB wzglę
mech2 153 304 F Zauważymy, że otrzymana wartość x Jest równa promieniowi bezwładności pręta AB wzglę
Notatki do lekcji, klasa matematyczna - Mariusz Kawecki, U LO w Chełmie Zauważmy, że alternatywa jes
więcej podobnych podstron