1105140589

Laboratorium problemowe, Model Helikoptera, Sprawozdanie.

<f>₀ = -0.543 [rad] d = 0.235 [m]

Zależność (1) to równanie różniczkowe nieliniowe, drugiego rzędu. Zakładając, że znana jest charakterystyka F(n), długość ramienia oraz kąt niewyważenia, na podstawie analizy odpowiedzi układu możliwa jest identyfikacja momentu bezwładności, współczynnika tarcia oraz momentu niewyważenia.

3.3.1 Moment niewyważenia

Identyfikacja momenty niewyważenia wykonano poprzez doświadczalne dobranie takiego sterowania, które utrzymuje belkę w pozycji zerowej. W takiej sytuacji równanie (1) przyjmuje postać:

-0.2281 [Nm]

0 = G sin(0—tj>_Q)+d ■ F(n) _c _ sin(^„) _ 0,009477 ~d-F(n)~    0.0415

3.3.2 Moment bezwładności oraz tarcia w osi zamocowania

Identyfikację momentu bezwładności oraz współczynnika tarcia wykonano dwiema metodami: metodą strojonego modelu oraz poprzez przybliżenie układu modelem liniowym drugiego rzędu (oscylator harmoniczny tłumiony)

Przesuwając układ współrzędnych tak, by kąt wychylenia belki przyjmował wartość zero w punkcie równowagi przy zatrzymanym śmigle, oraz linearyzując model w tymże punkcie, równanie (1) przyjmuje postać:

xl = Gx- /3x

Można wykazać, że dla układu opisanego powyższym równaniem różniczkowym:

(2)

J =

GT²

4k² +A²'

Gdzie T to okres drgań tłumionych, a A to dekrement tłumienia opisany zależnością [Ą- i-ta amplituda drgań):

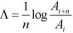
Zarejestrowano swobodne oscylacje belki.

Strona 13 z 27