2212790602

2. Sprawdzić trzema metodami, czy formula jest tautologią.

(a)    p =► (p => q)

(b)    (p A q) => (p V g)

(c)    (p A g) V (p => g)

(d)    (p=j»g)=>(~pVg)

(e)    (pA~g)=s-~(p^g)

Odpouńedź: Tautologiami są formuły: b, d, e.

3.    Sprawdzić trzema metodami, czy formula jest kontrtautologią.

(a)    (p V g) A (p A ~ g)

(b)    (p A g) A (p ~ g)

(c)    pA~(p=> g)

(d)    ~ [p =» (p => ~ g)]

(e)    ~(pVg) A(~p=>g)

Odpowiedź: Kontrtautologiami są formuły: b, e.

4.    Sprawdzić metodą skróconą, czy formuła jest tautologią.

(a)    (p g) =► [(p =*• g) V g]

(b)    [(p =>■ g) A g] => (p <=> g)

(c)    (p =► g) (~ g =► ~ p)

(d)    (~ p =► g) (g => p)

(e)    [(pA~g)A(g»~ r)] => r

(f)    \p => (g A r)] => [~ g => (p V ~ r)]

(g)    (P => g) =► {(P => r) => Jp => (g A r)]}

Odpowiedź: Tautologiami są formuły: a, c, e, g.

5.    Sprawdzić metodą skróconą, czy formuła jest kontrtautologią.

(a)    (p g) A ~ (p => g)

(b)    ~ [p => (~ g Ar)] A (p => r)

(c)    (p => g) A (~ g => ~ r) A ~ [(p V r) => g]

Odpowiedź: Kontrtautologiami są formuły: a, c.

2.1.2 Konsekwencje logiczne

1. Sprawdzić poprawność wnioskowania: Je'sli funkcja ma pochodną, to jest ciągła, a je'sli funkcja jest ciągła, to ma pochodną, a więc funkcja ma pochodną, wtedy i tylko wtedy, gdy jest ciągła.

Rozwiązanie:

• schemat wnioskowania można zapisać w trzech postaciach:

P => 9

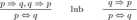
{? =► 9.9 =>■ P) 1= P <=* 9

gdzie p — funkcja ma pochodną, q — funkcja jest ciągła, korzystamy z definicji konsekwencji logicznej:

Istnieją dwa modele i w każdym z nich wniosek jest prawdziwy.