2659242007

2.3 Modele mieszane

Model mieszany zakłada, że istnieją zarówno stany ciągłe jak i dyskretne. Stany dyskretne są opisane poprzez równania różniczkowe zwyczajne, natomiast stany ciągłe przez równanie transportu z odpowiednim warunkiem brzegowym. Na przykład, dla kombinacji dwóch stanów dyskretnych, połączonych stanami ciągłymi, otrzymujemy ([7]):

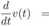
dtu(t,x) + d_x(g(t,x)u(t,x)) =

5(0, x)u(0,x) =

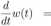
P„(t)v(f) - 9v(t)v(f) p(t,x)u(t,x), dla a: e [xo,a;*] 9v{t)v(t)

p_w(t)w(t) + g(t, x*)u(t, x*).

Układ ten interpretujemy następująco: komórka w stanie opisywanym zmienną v, jeśli się zróżnicuje, przechodzi do stanu xo- Następnie podąża (być może po drodze rozmnażając się) przez wszystkie stany x 6 [xo, £*], by ostatecznie z x* zróżnicować się do stanu w, gdzie może się już tylko dzielić lub umrzeć.

3 Metodologia badań

3.1 Problemy badawcze

Główne pytanie, na które odpowiada niniejsza dysertacja jest następujące:

Jak w jednolity, przejrzysty i pozwalający łatwo dostrzegać zależności sposób zapisać różne modele procesu różnicowania się komórek?

By odpowiedzieć na to pytanie, przyjmujemy następującą strategię.

1.    Identyfikujemy wspólne własności dyskretnych i ciągłych modeli różnicowania się komórek.

2.    Wykorzystując te własności, zapisujemy modele ciągłe, dyskretne i mieszane w jednej, wspólnej postaci, zanurzając je w ciągłe równanie transportu.

3.    Interpretujemy powstałą strukturę jako proces stochastyczny lub przepływ miary.

4.    Wykazujemy istnienie i jednoznaczność rozwiązań równań zanurzonych modeli mieszanych.

5.    Proponujemy motywowaną biologicznie metrykę, która dobrze opisuje zarówno przypadki stabilności, jak i destabilizacji rozważanego procesu.

6.    Dowodzimy stabilności w metryce zanurzonego modelu mieszanego.

7.    Wprowadzamy diagramatyczny zapis całek, który ułatwia przeprowadzanie, czytanie i interpretację dowodów.

8.    Identyfikujemy własności zanurzonego modelu dyskretnego, które prowadzą do nowych problemów badawczych.

5