2749771996

Kody wykrywające i korygujące błędy - konspekt wykładu 2006/07    14

Twierdzenie 2.10. (Ograniczenie Singletona.)

Jeśli C jest (n, k, d) -kodem liniowym to

n — k ^ d — 1.

Twierdzenie 2.11. (Ograniczenie Gilberta - Varshamova.)

Istnieje binarny kod liniowy długości n z co najwyżej r symbolami kontroli parzystości i odległością co najmniej d taki, że

1 +

n — 1 d-2

< 2^r.

Można pokazać, że istnieje kod liniowy nad ciałem GF(q) o tych samych własnościach taki, że

d—2

Et?-¹)'

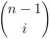
<q^r.

2=0

Twierdzenie (2.11) dowodzi, że istnieją dobre kody liniowe, ale nie wskazuje metody ich konstrukcji.

Twierdzenie 2.12. (Ograniczenie Griesmera.)

Najkrótszy binarny kod liniowy wymiaru k i odległości d ma co najmniej długość X)i=o¹r^'l- (\^x~\ J^est najmniejszą liczbą całkowitą większą od x.)

Przykład 2.13. Najkrótszy kod liniowy wymiaru 5, poprawiający błędy potrójne ma długość równą co najmniej

4    ?    7    7    7    7

Ey = ₇₊ y + \n ₊ \^ = i5.

Istnieje liniowy (15,5,7)-kod BCH.

Definicja 2.14. (n,n — k)-kod liniowy C¹ := {u G Aⁿ \ uw = 0, w G C} nazywamy kodem dualnym lub kodem ortogonalnym do C.

(uw := UiWi w ciele GF(q).)

2=1

Jeśli H jest macierzą kontroli parzystości a G macierzą generującą kodu C to H^T jest macierzą generującą a G^T jest macierzą kontroli parzystości kodu dualnego C¹.