2749771998

Kody wykrywające i korygujące błędy - konspekt wykładu 2006/07    16

Zatem wektory y i e należą do tych samych warstw względem podprzestrzeni C.

Stosując strategię dekodowania z maksymalną wiarygodnością odkodujemy wektor y jako najbliższe mu w sensie odległości słowo kodowe u. Wektor błędu będzie miał wtedy najmniejszą możliwą wagę. Zauważmy, że gdy H jest macierzą kontroli parzystości kodu C to

Hy = H{v + e) = Hv + He = He,

czyli syndrom Hy wektora y jest taki sam jak syndrom He wektora błędu e. Zatem po otrzymaniu słowa y wybieramy wektor błędu e o minimalnej wadze w tej warstwie do której należy wektor y (tzw. lidera warstwy) i dekodujemy y jako słowo v = y — e. Jeśli istnieje więcej niż jeden wektor o minimalnej wadze w danej warstwie, to lidera warstwy wybieramy losowo.

Jeśli słowo y G C ma wagę w, to syndrom Hy jest kombinacją liniową pewnych w kolumn macierzy H. Jeśli wektor e jest wektorem błędu to syndrom He jest kombinacją liniową tych kolumn macierzy H, na których został popełniony błąd. Jeśli wystąpił tylko pojedynczy błąd na i-tym miejscu to wektor błędu e = 0... b... 0 ma wagę 1 i syndrom He jest i-tą kolumną macierzy H pomnożoną przez stałą b. Gdyby i-ta kolumna macierzy H była zerowa to błąd występujący na i-tej pozycji nie zostałby wykryty. Ponadto dla kodów binarnych, jeśli dwie kolumny macierzy H byłyby identyczne, to dwa syndromy dla dwóch różnych błędów pojedynczych byłyby takie same. W obu tych przypadkach nie byłoby możliwe wykrycie błędów pojedynczych. Stąd macierz kontroli parzystości H dla binarnych kodów wykrywających błędy pojedyncze musi mieć kolumny parami różne i niezerowe.

Przykład 2.20. Macierz

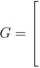
jest macierzą generująca binarnego (4,2)-kodu liniowego C. Wszystkie 16 binarnych wektorów długości 4 możemy podzielić na cztery warstwy względem