5466967406

123.    Niech przekształcenie liniowe /: V —> V ma w bazie \vi,vi,vz} macierz A. Jaką macierz ma / w bazie {ui +t>2, v-i + vs, 1/3}?

124.    Niech f:V—>W będzie przekształceniem liniowym. Wykazać, że jądro ker / i obraz Im / są podprzestrzeniami liniowymi oraz dim V = dim ker / + dim Im /.

125.    Wyznaczyć zbiór rozwiązań układu równań (nad ciałem R)

X\ — 2X2 + 3^3 ^— 4x4 = 5 Xl + 2X2 + 3X3 + 4x4 = —10

4xi + 12x3 = t

w zależności od parametru t € R.

126. Niech a,b,c 6 R. Załóżmy, że zbiór rozwiązań układu równań

axi + 6x2 = c axi + 0x3 = b bx 2 + 0x3 = a

jest jednoelementowy. Wykazać, ze abc ^ 0 i znaleźć rozwiązanie powyższego układu.

127.    Znaleźć macierz przekształcenia sprzężonego do /(x, y) = (x — y, 2x) w bazie (R²)* sprzężonej do bazy {(1,1), (1,2)} przestrzeni R².

128.    Wyznaczyć postać Jordana macierzy

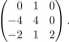
129.    Podać definicję wielomianu charakterystycznego endomorfizmu / skończenie wymiarowej przestrzeni liniowej V nad ciałem K. Uzasadnić, że definicja ta nie zależy od wyboru bazy w przestrzeni V.

130.    Podać definicję śladu endomorfizmu / skończenie wymiarowej przestrzeni liniowej V nad ciałem K. Wykazać, że definicja ta nie zależy od wyboru bazy w przestrzeni V.

131.    Niech / będzie niezerowym endomorfizmem przestrzeni liniowej V takim, że /³ jest odwzorowaniem zerowym. Wykazać, że nie istnieje baza, w której / ma macierz diagonalną.

132.    Sprawdzić, czy zbiory punktów {(1,1,0), (2,1,0), (3,1,1)} i {(2,1,0), (3,1,0), (3,1,1)} rozpinają w R³ tę samą podprzestrzeń afiniczną.

133.    Podać wzór na obrót płaszczyzny R² o kąt f wokół punktu (1,1).

134.    Forma dwuliniowa £ : R³ x R³ —» R ma w bazie standardowej macierz

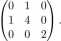
Obliczyć £((1,2,0), (2,0,1)).

135. Sprawdzić, czy forma dwuliniowa zadana w bazie standardowej macierzą

zadaje na R³ pewien iloczyn skalarny.

10