7355923243

Analiza input - oulpul. Notalki S. Dorosiewicz, J. Slasieńko Strona 15 z 28

Analiza input - oulpul. Notalki S. Dorosiewicz, J. Slasieńko Strona 15 z 28

" 20	10	30 '
100	150	160
25	45	45
100	150	160
15	60	15
.100	150	160.

W notacji macierzowej układ ten ma postać:

m		an	^a\n	x{		r,
X„	-	^an\	■' ^arm	x„	+	Y„

III o wartości odpowiednio 20, 25 oraz 15 (j.p). Należy spodziewać się, że w okresie t+5, gdy wartość produkcji podwoi się, podwoją się także odpowiednie nakłady (a więc elementy pierwszej kolumny macierzy przepływów międzygałęziowych [xy]. Wynika stąd, że wartość produkcji zużytej w gałęzi I będzie równa 40, 50 i 30 (j.p). Podobnie należy spodziewać się, że wartości surowców zużytych do produkcji w gałęzi II (a więc wartości elementów drugiej kolumny macierzy foj]) wzrosną 1,5 - krotnie. Elementy drugiej kolumny macierzy przepływów międzygałęziowych będą zatem równe kolejno: 15, 67.5 oraz 90 (j.p.). Elementy trzeciej kolumny nie ulegają zmianie.    Macierz przepływów

międzygałęziowych [Xjj] dla roku t+5 ma zatem postać:

'40    15    30'

50 67.5 45 .

30    90    15

• Pozostałe elementy bilansu, a więc wartości dodane i produkcje końcowe możemy łatwo wyznaczyć z pomocą równań bilansowych. Ostatecznie przewidywany dla roku t+5 bilans dla rozważanego układu ma postać przedstawioną w prezentowanej tablicy

Xi	Xii			Yi
200	40	15	30	115
225	50	67.5	45	62.5
160	30	90	15	25
	80	52.5	70
_S_	200	225	160

W dalszej części przedstawimy równania modelu prowadzące do szybkiego wyznaczania elementów bilansu. Potrzebna nam będzie macierz struktury kosztów.

MACIERZ STRUKTURY KOSZTÓW

Macierzą struktury kosztów (lub krócej macierzą kosztów dla n - gałęziowego układu gospodarczego nazywamy macierz A = [Oy]_nxn o elementach zdefiniowanych wzorem

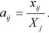
Zauważmy, że gdyby produkcja globalna X, miała wartość jednostkową, to a_tJ byłoby równe wartości odpowiedniego przepływu międzygałęziowego. Wynika stąd następująca interpretacja elementów macierzy kosztów: element a_l] jest równy wartości produkcji i - tej gałęzi zużywanej w gałęzi j w celu wytworzenia w tej gałęzi produktu globalnego o wartości jednostkowej (1 j.p).

PRZYKŁAD

Dla układu gospodarczego opisanego w poprzednim przykładzie macierz kosztów dla roku t jest równa zaś dla okresu t+5:

' 40	15	30'
200	225	160
50	67.5	45
200	225	160
30	90	15
.200	225	160.

Oczywiście zachodzi równość

A, = 4_+s,

która wyraża uczynione przez nas, na początku omawiania modelu Leontiewa, założenie o niezmienności relacji pomiędzy nakładami a wynikami produkcji.

RÓWNANIE MODELU LEONTIEWA

Przekształcając równości

^xn

do postaci

x_y =a_jjXj,

możemy układ równań bilansowych

X, = +Y_t (7 = 1,..., ri)

j=i

zapisać w postaci

X, = Za_JX_J+Y_l (7 = 1,.., Ti).

czyli

X = AX + Y,

gdzie X, Y oznaczają odpowiednio wektor wartości produkcji globalnej i końcowej.

Ostatnie równanie można zapisać w postaci

Instytut Ekonometrii SGH