7355923249

Analiza input - output. Notatki S. Dorosicwicz, J. Stasieńko Strona 20 z 28

warunki nieujemności wynikające z określenia zmiennych decyzyjnych:

*, >0, *₂>0.

Kryterium wyboru decyzji optymalnej stanowi maksymalizacja łącznej wartości produkcji końcowej Y = Y_t +Y₂.

Ponieważ

Y_{ = 0,8*, ~ 0,4X₂,

Y₂ = -0,3X_l + 0,9X₂,

więc

7=0,5*, + 0,5*₂.

Zadanie sprowadza się zatem do znalezienia pary liczb    (*,, X₂) maksymalizujących

wartość wyrażenia

0,5*, + 0,5*₂

i spełniających warunki:

*, < 60,

*, <80;

2*, - *₂ > 0,

-*, + 3*2 > 0,

-*, + —*₂ <35,

4 ¹    3 ²

*, >0,

*₂ >0.

3. Rozwiązanie zadania

Rozwiążemy teraz sformułowany problem. Z uwagi na to, że mamy dwie zmienne decyzyjne, a parze liczb (X!, X₂) odpowiada jednoznacznie punkt na płaszczyźnie, zadanie powyższe rozwiążemy metodą graficzną.

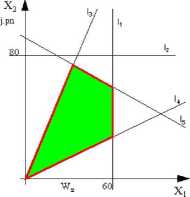
Wprowadźmy na płaszczyźnie prostokątny układ współrzędnych w którym na osi odciętych będą odkładane wartości *,, a na osi rzędnych - wartości X₂. W ten sposób każdej decyzji (*,,*₂) odpowiada punkt na płaszczyźnie o odpowiednich współrzędnych. Każdy z warunków ograniczających wyznacza pewną półpłaszczyznę, zbiór decyzji dopuszczalnych jest zaś częścią wspólną tych półpłaszczyzn. Na rysunku podano interpretację geometryczną zbioru decyzji dopuszczalnych, zaznaczając dodatkowo krawędzie półpłaszczyzn wyznaczonych przez kolejne warunki (proste /,, l₂...)

j.pn.

Graficzna interpretacja zbioru decyzji dopuszczalnych.

Proste li.....I₅ są krawędziami płaszczyzn

wyznaczanych przez kolejne warunki ograniczające modelu. W przypadku dwu ostatnich warunków prostymi tymi są osie układu współrzędnych. Zakreskowany obszar, będący częścią wspólną tych płaszczyzn odpowiada zbiorowi decyzji dopuszczalnych.

Gradient funkcji celu, wskazujący kierunek najszybszego wzrostu wartości tej funkcji, ma współrzędne [0,5; 0,5]. Warstwice funkcji celu są prostymi prostopadłymi do tego wektora i mają równania 0,5*, +0,5*₂ =c, gdzie c może być dowolną liczbą rzeczywistą.

W celu wyznaczenia decyzji optymalnych szukamy warstwicy funkcji celu odpowiadającej możliwie największej wartości c (a więc wartości funkcji celu) i mającej ze zbiorem decyzji dopuszczalnych co najmniej jeden punkt wspólny. W tym celu przesuwamy „w górę” prostą prostopadłą do gradientu funkcji celu, to znaczy w kierunku wskazywanym przez ten wektor. Stwierdzamy, że zadanie ma jedną decyzję optymalną - jest nią (*,, *₂) = (60, 60).

Instytut Ekonometrii SGH