7355923247

Analiza input - oulpul. Notalki S. Dorosiewicz, J. Slasieńko Strona 19 z 28

X		1,96	1,60	1,35'	20^_		143,6
		0,32	1,41	0,38	40	*	74,4
Y,		0,93	1,09	2,12	30_		125,6

Aby zwiększyć wartość produkcji końcowej w każdej z gałęzi o 5 j.p., produkcja globalna powinna wzrosnąć o około: 24,5 j.p. w gałęzi I, 10,6 j.p. w gałęzi II oraz 20,7 j.p. w III gałęzi. Wnioski te otrzymujemy z równania L~'AY = AA”, tzn.

AYX		1,96	1,60	1,35'	5		24,5‘
A Y2	*	0,32	1,41	0,38	5	*	10,6
A 7,		0,93	1,09	2,12	5		20,7

Załóżmy, że produkcja globalna I gałęzi ma wartość 200 j.p., a produkcja końcowa II i III gałęzi odpowiednio 50 oraz 60 j.p. Rozwiązując równanie

0,8	-0,6	-0,4	200		Yx
-0,1	0,9	-0,1		=	50
-0,3	-0,2	0,7	*3		60

widzimy, że w takiej sytuacji produkcja globalna gałęzi II i III jest równa odpowiednio 100 oraz 200 j.p, a produkcja końcowa I gałęzi ma wartość 20 j.p.

OPTYMALIZACJA I MODEL LEONTIEWA

Modelem Leontiewa zbudowanym dla określonego układu gospodarczego posłużyć się można do usprawniania funkcjonowania tego układu.

Równanie modelu

X=AX+Y

ma nieskończenie wiele rozwiązań: zadając różną produkcję końcową Y otrzymujemy różne wartości niezbędnej dla jej uzyskania produkcji globalnej X. Innymi słowy równanie modelu określa wiele różnych rozwiązań (X,Y), które można interpretować jako wewnętrznie zgodne plany produkcji. Można więc rozważać zagadnienie wyboru takiego planu, czy planów, które są najlepsze z punktu widzenia przyjętego kryterium, na przykład maksymalizacji produkcji końcowej całego układu gospodarczego lub jego wybranych gałęzi.

W zamieszczonym niżej przykładzie omówimy sposób podejmowania decyzji w oparciu o model Leontiewa. Rozpoczniemy od opisu problemu decyzyjnego, następnie dokonamy jego formalizacji w postaci modelu matematycznego, który pozwoli na znalezienie decyzji optymalnych.

1. Opis problemu decyzyjnego

Rozważmy kraj o dwugałęziowej, samowystarczalnej gospodarce. W założeniach rozwoju gospodarczego założono, iż zdolność wytwórcza gałęzi I wynosi 60 j.p, a gałęzi II 80 j.p. Relacje między nakładami i wynikami, określają następującą macierz kosztów:

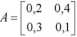
Udział kosztów robocizny w globalnej wartości produkcji powinien kształtować się na poziomie 1/4 oraz 1/3 odpowiednio w gałęzi I oraz II, a łączny fundusz płac nie powinien przekroczyć 35 j.p.

Problem polega na ustaleniu wartości produkcji globalnej w obu gałęziach, aby wartość produkcji końcowej gospodarki była możliwie największa.

2. Model matematyczny problemu

Zmiennymi decyzyjnymi będą wartości (w j.p.) produkcji globalnej *,, X₂ odpowiednio pierwszej i drugiej gałęzi układu.

Każdej decyzji odpowiada para liczb (*,,*₂). Znajdźmy zbiór decyzji dopuszczalnych, to znaczy spełniających sformułowane ograniczenia, ograniczenia dla maksymalnej wartości produkcji globalnej:

*, <60,

X_x <80;

warunek samowystarczalności gospodarki oznacza, że wartości produkcji końcowej Y_x,Y₂ są nieujemne:

LX > 0,

gdzie L oznacza macierz Leontiewa.

W rozważanym przypadku mamy _ I" 0,8    -0,4]

”|_-0,3 0,9j’ dlatego ograniczenia mają postać 0,8*, - 0,4*₂ > 0,

-0,3*, + 0,9*₂ > 0, ograniczenia dla funduszu płac:

Instytut Ekonometrii SGH