1109810453

EGZAMIN MAGISTERSKI, 18.09.2012 Zastosowania

Zadanie X • (8 punktów)

Niech X_n,Y_n będą wzajemnie niezależnymi zmiennymi losowymi o rozkładach y²(n) oraz N(n,n) (wariancja wynosi n) odpowiednio. Zbadać zbieżność ilorazu

Xn

Yn

gdy n —► oo. Odpowiedź uzasadnić.

Zadanie £ • (8 punktów)

Dla procesu Poissona Nt z intensywnością 1 oraz dla s>t znajdź v(n) — E[N_s\Nt — n].

Zadanie O • (8 punktów)

Niech    Ag będą niezależnymi zmiennymi losowymi o tym samym rozkadzie

B(ar, 1) i gęstości:

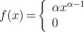
0< x < 1 poza tym,

(i)

gdzie a > 0 jest nieznanym parametrem. Weryfikujemy hipotezę H₀ : a — 1 przy alternatywie Hi: a > 1 testem jednostajnie najmocniejszym na poziomie istotności p= 0,05. Wyznacz jego moc przy a — S jeśli Xi2^-1(0i05) =5,23 oraz Xi2(3 x 5,23) = 0,79, gdzie Xj₂(') oznacza dystrybuantę rozkładu Xi2-

Zadanie 4* (8 punktów)

Sprawdź, że (R,d) jest przestrzenią metryczną dla

d(x,y) = min(l,\x-y\).

Co możesz powiedzieć o zupełności i ośrodkowoci tej przestrzeni?

Zadanie O • (8 punktów)

Wszystkie wartości funkcji holomorficznej /:€ —»C leżą na ustalonej prostej. Udowodnij, że / jest stała.